引言本章的重点内容是编译器的前端技术的总体介绍,特别是词法分析、语法分析和中间代码生成。对于本章节的笔记,我会分为两个部分:上半...

引言
本章的重点内容是编译器的前端技术的总体介绍,特别是词法分析、语法分析和中间代码生成。
对于本章节的笔记,我会分为两个部分:上半篇主要侧重点会在相关概念和技术的理解上,下半篇将会是一个动手实践——一个简单的编译器前端实现。
语法定义
分析阶段的工作是围绕着待编译语言的“语法”展开的,而一个被广泛使用描述语法的表示方法,就是上下文无关文法,简称文法。
上下文无关文法
文法自然的描述了大多数程序设计语言构造的层次化语法结构。例如,Java 中的 if-else 语句具有如下的一般形式:
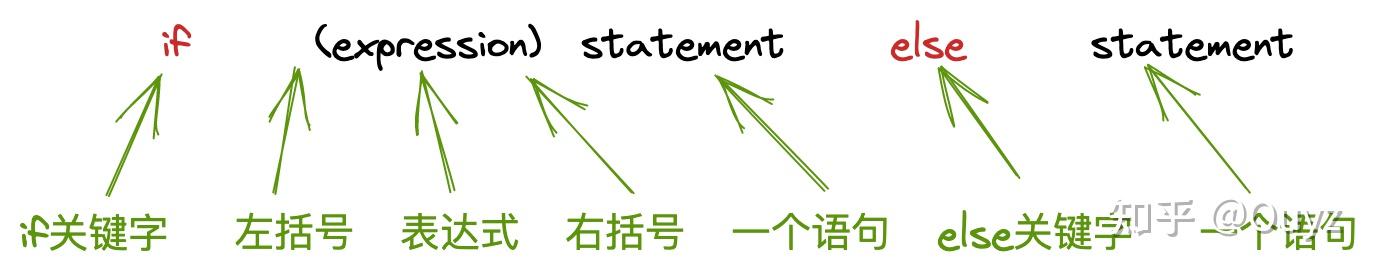

如果我们用变量 expr 来表示表达式,用变量 stmt 表示语句,那么这个 if-else 语句的构造规则可以表示为
其中的箭头(→)可以读作“可以具有如下形式”,这样的规则我们称为「产生式(production)」。在产生式中,像关键字 if 和括号这种词法元素我们称之为「终结符号(terminal)」。像 expr 和 stmt 这样表示终结符号序列的变量,我们称之为「非终结符号(nontermial)」。
文法定义
文法的定义:描述语言的语法结构的形式规则(即语法规则)。
一个上下文无关文法(context-free grammar,CFG)由四个元素组成(即四元组:):
- 终结符号集合(
):有时也被称为“词法单元集合”,终结符号是该文法所定义的语言的基本符号的集合。
- 非终结符号集合(
):有时也被称为“语法变量”,每个非终结符号表示一个终结符号串的集合。
- 产生式集合(P):其中每个产生式包括一个称为产生式头或左部的非终结符号,一个箭头,和一个称为产生式体或右部的由终结符号组成的序列。产生式主要用来表示某个构造的书写形式。如果产生式头部非终结符号代表一个构造,那么该产生式体 就代表该构造的书写形式。
- 指定一个非终结符号为开始符号(S)。
我们通过一个简单的例子来具体说明文法定义的过程。
我们有一些由数位和 + 、 - 符号组成的表达式,比如 9 - 5 + 2、3 - 1 或 7 等。由于两个数位之间必须出现 + 或 -,我们把这样的表达式称为“由 + 、- 号分隔的数位序列”。我们可以使用这样一种文法描述此类表达式的语法:
以非终结符号 list 为头部的三个产生式可以等价地组合为:
所以在上面的这个例子中:
- 该文法的终结符号包括如下符号:
+ - 0 1 2 3 4 5 6 7 8 9 - 该文法的非终结符号是:
list和digit。因为list的产生式首先被列出来,所以我们知道list是此文法的开始符号。 - 若是以一个具体的表达式为例,比如:
9 - 5 + 2经过词法分析产生的词法单元序列为:<digit, 9> + <digit, 5> + <digit + 2>。可以看到词法单元由 <名字,属性> 组成,我们常常把名字部分称为终结符号。
此外,一个终结符号串是由零个或多个终结符号组成的序列,零个终结符号组成的串称为空串(empty string),记为 ε。
推导
在本节主要是引入几个概念和术语:
这里我们还是举一个表达式的例子(9 - 5 + 2)来简单说明一下最左推导和最右推导之间的区别:
最左推导:
最右推导:
语法分析树
给定一个上下文无关文法,该文法的一棵语法分析树(parse tree)是具有以下性质的树:
1)根节点的标号为文法的开始符号。
2)每个叶子结点的标号为一个终结描述符号或 ε 。
3)每个内部节点的标号为一个非终结符号。
4)如果非终结符号A是某个内部结点的标号,并且它的子结点的标号从左至右分别为 ,那么必然存在产生式
,其中,
既可以是终结符号,也可以是非终结符号。作为一个特殊的情况,如果
是一个产生式,那么一个标号为
的结点可以只有一个标号为
的子结点。
还是以上面的表达式 9 - 5 + 2 为例,根据上面描述的表达式文法可以得到一颗语法分析树:
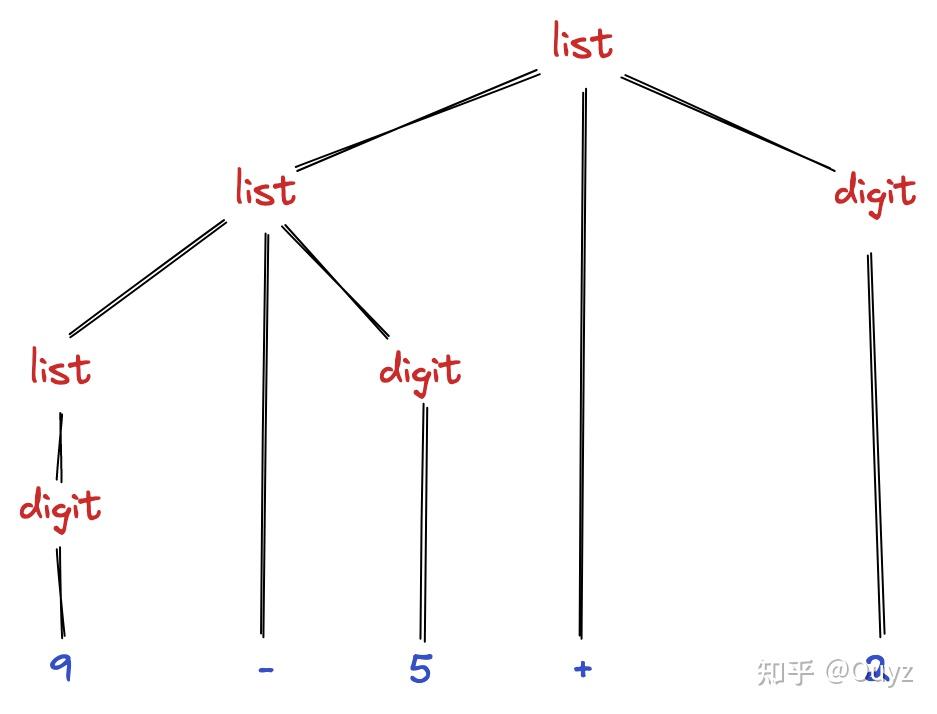

可以看到在这个例子中,我们把叶子结点都放在了底层(这里只是为了方便,以后可能不按这种方法排列),从左到右构成了树的结果(yield)9 - 5 + 2。
所以从语法分析树的角度,我们可以重新定义上面的三个概念:
二义性
一个文法可能有多棵语法分析树能够生成同一个给定的终结符号串,这样的文法称为具有二义性(ambiguous)。
同样还是上面的“由 + 、- 号分隔的数位序列”的表达式例子,我们这里举一个具有二义性文法的例子,我们将 list 和 digit 合并为一个非终结符号 string,那么我们可以得到如下的产生式:
所以同样一个表达式 9 - 5 + 2,我们可以推导得到两个不同的语法分析树:
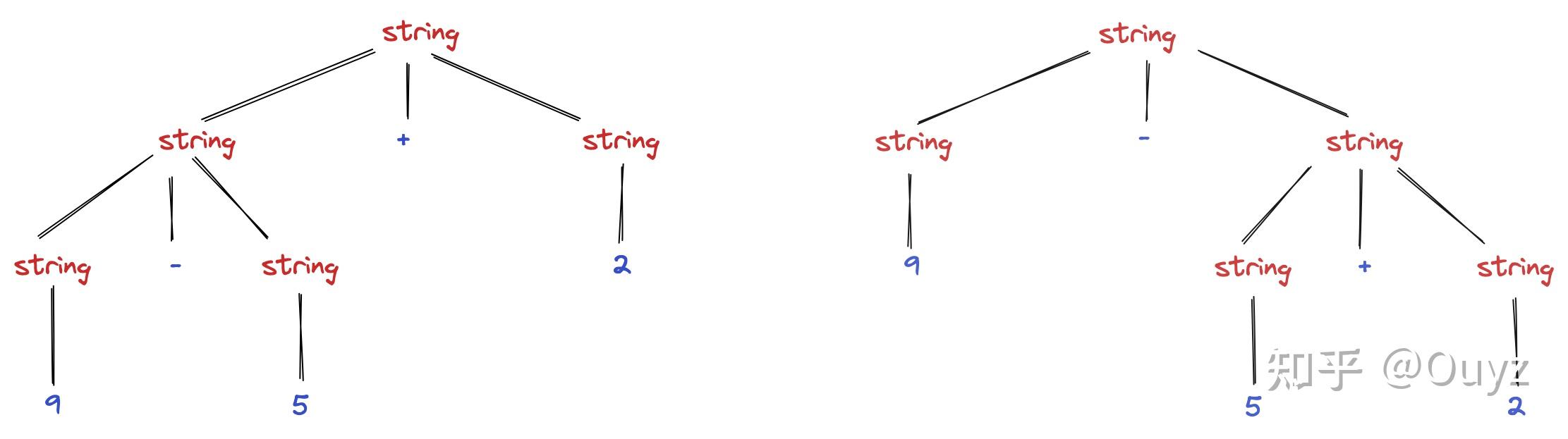

这里需要补充的一点是「语法分析树的形状和推导方法无关,只和文法定义有关」。
关于如何判断一个文法是否具有二义性以及如何消除二义性我们会在之后的章节中在深入探讨。
运算符的结合性
当一个运算分量的左右两侧都有运算符时,我们需要一些规则来决定哪个运算符被应用于该运算分量。
在大部分的程序语言中,加、减、乘、除四种算术运算符都是左结合的,另外一些常用运算符是右结合,比如指数运算或者赋值运算。
以 9 - 5 - 2 和 a = b = c 为例子,下图对比了左结合和右结合得到的语法分析树的区别,首先 a = b = c 可以由如下文法产生:
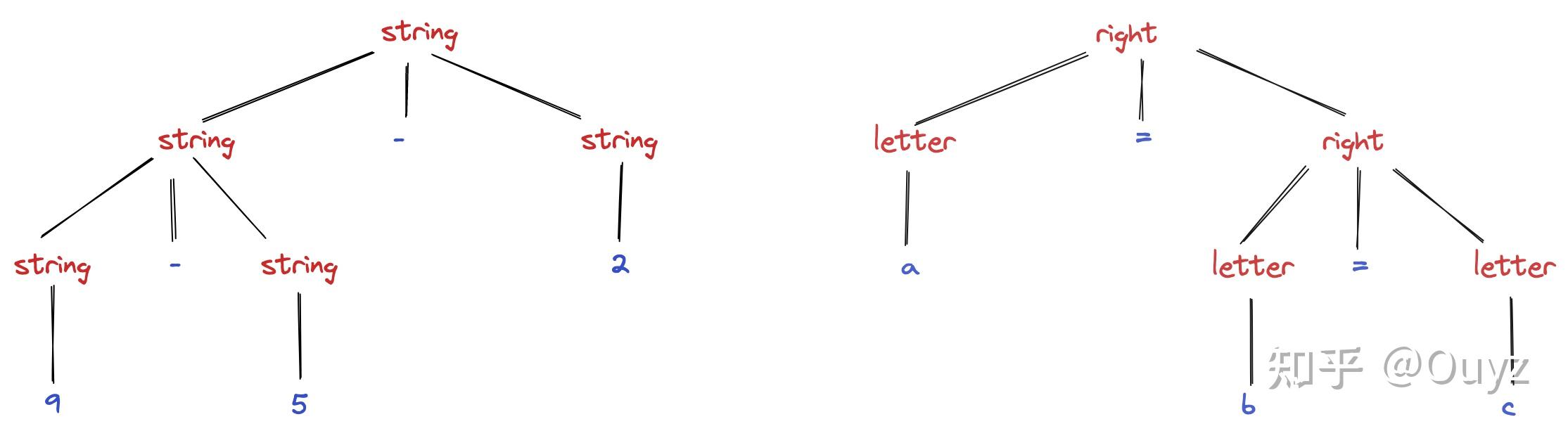

可以看到左结合的语法分析树向左下延伸,而右结合的语法分析树向右下延伸。
运算符的优先级
当多种运算符出现的时候,我们需要给出一些规则来定义运算符之间的优先级关系。
如果 * 先于 + 获得运算分量,我们就说 * 比 + 具有更高的优先级。我们来看一下一个简单算术表达式的文法表示:
我们创建两个非终结符 expr 和 term,分别对应这两个优先级层次。另外,使用 factor 来生成表达式中基本单元。
表达式中的基本单元是数位和带括号的表达式:
接下来是最高优先级的二目运算符 * 和 / ,这些运算符是左结合,产生式如下:
类似地,expr 生成由加减运算符分隔的 term 列表:
因此最终得到的文法是:
我们可以把上面的文法定义推广到具有任意 n 层优先级的情况:
- factor 描述的不可分开的基本单元。
- 然后,对于每个优先级都有一个非终结符号,表示能够被该优先级或更高优先级的运算符分开的表达式。通常:
- 该产生式有些产生式体表示了该优先级运算符的应用
- 另有一个产生式体只包含代表更高一层优先级的非终结符号。
语法制导翻译
什么是语法制导翻译?
在编译器前端组成部分中,语义分析和中间代码生成往往在实现上经常放在一起,称为语义翻译。此外,我们还可以在语义分析的时候进行语义翻译,这个过程就称为语法制导翻译,如图:
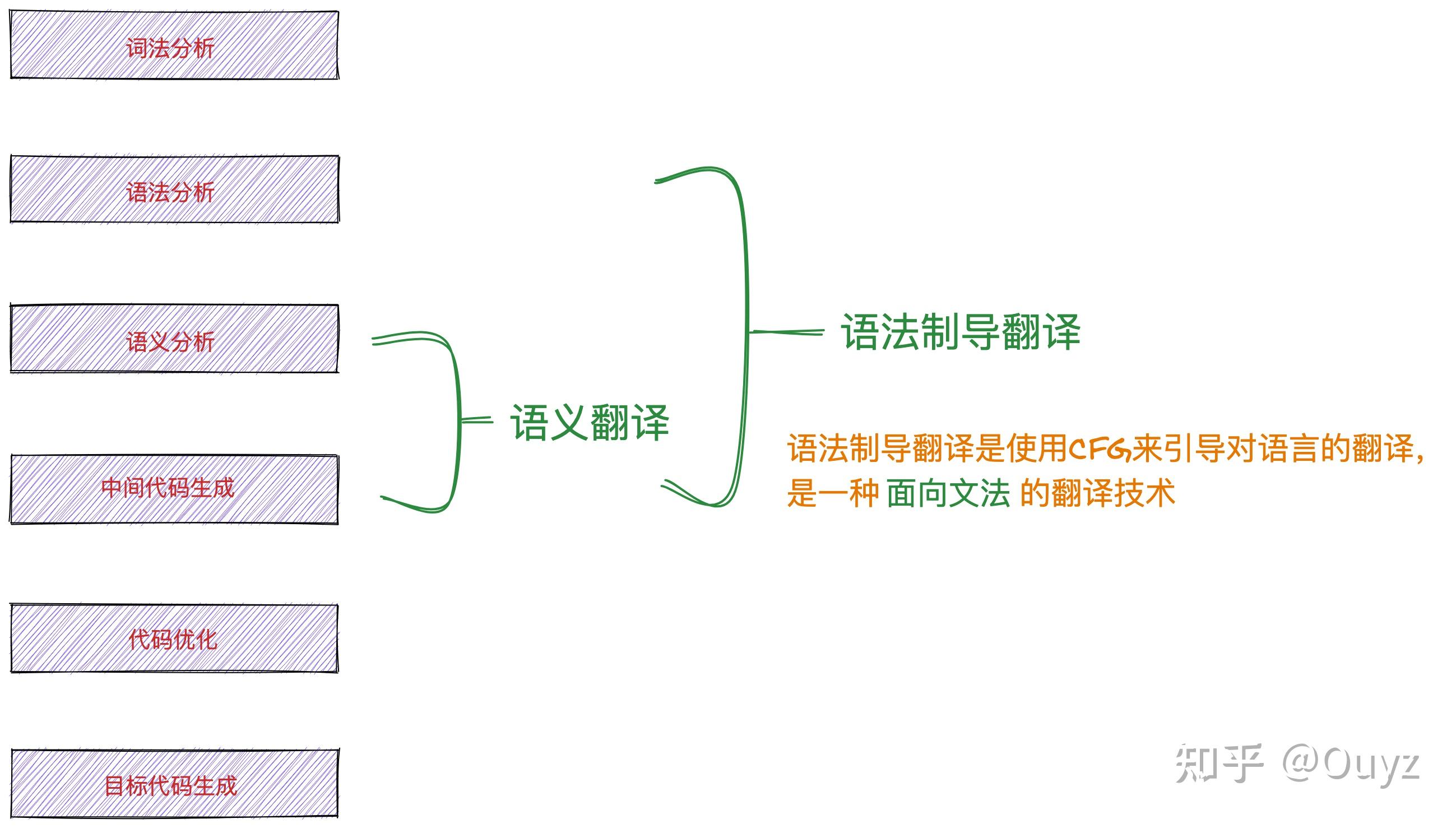

如何表示语义信息?
在前面的小节中,我们已经了有语法规则的形式化定义——文法,那么我们应该如何进行语义分析呢?在这之前我们先考虑一个问题,应该如何表示语义信息呢?
在这里就需要引入两个概念了:
通过引入这两个概念,我就可以将语义规则同语法规则(产生式)联系起来了,相应的我们可以得到以下两个表示语义信息的方式:
什么是语法制导定义(SDD)
语法制导定义是对 CFG 的推广:
具体的,我们以书中的处理中缀表达式(忽略括号处理)到后缀表示的翻译为例( 9 - 5 + 2 翻译为 95 - 2 +):
假设语法分析树的一个结点 N 的标号为文法符号 X,我们用 X.a 表示该结点上 X 的属性 a 的值。如此我们可以给分析树的各个结点标记相应的属性值,得到一颗注释分析树:
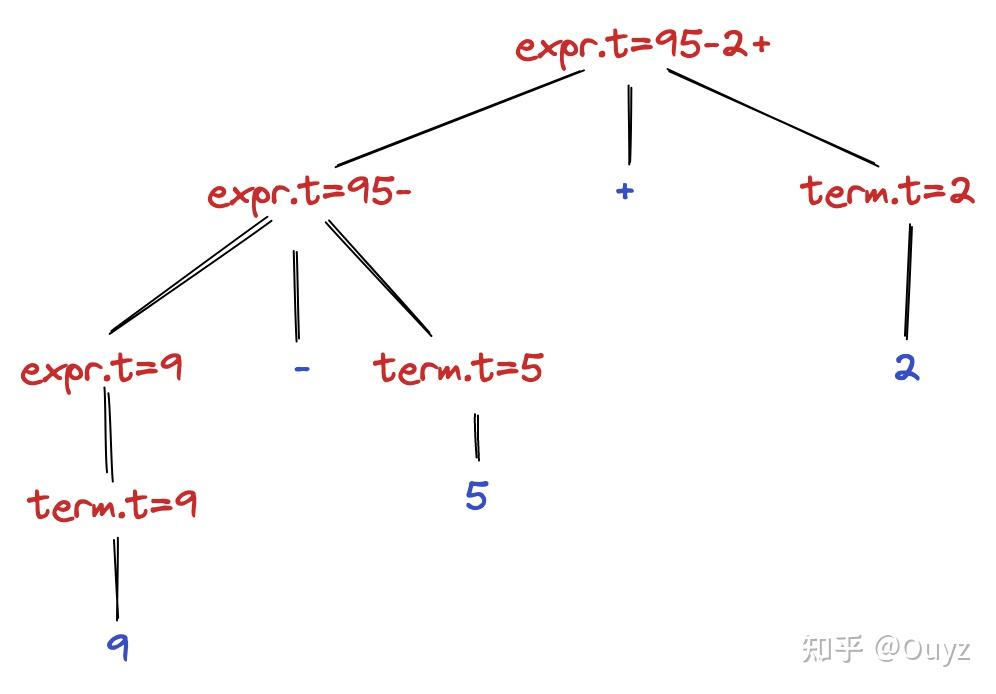

至于上面的语法分析树各个结点的属性值计算,由以下的语义规则给出(其中 || 表示字符串拼接操作):
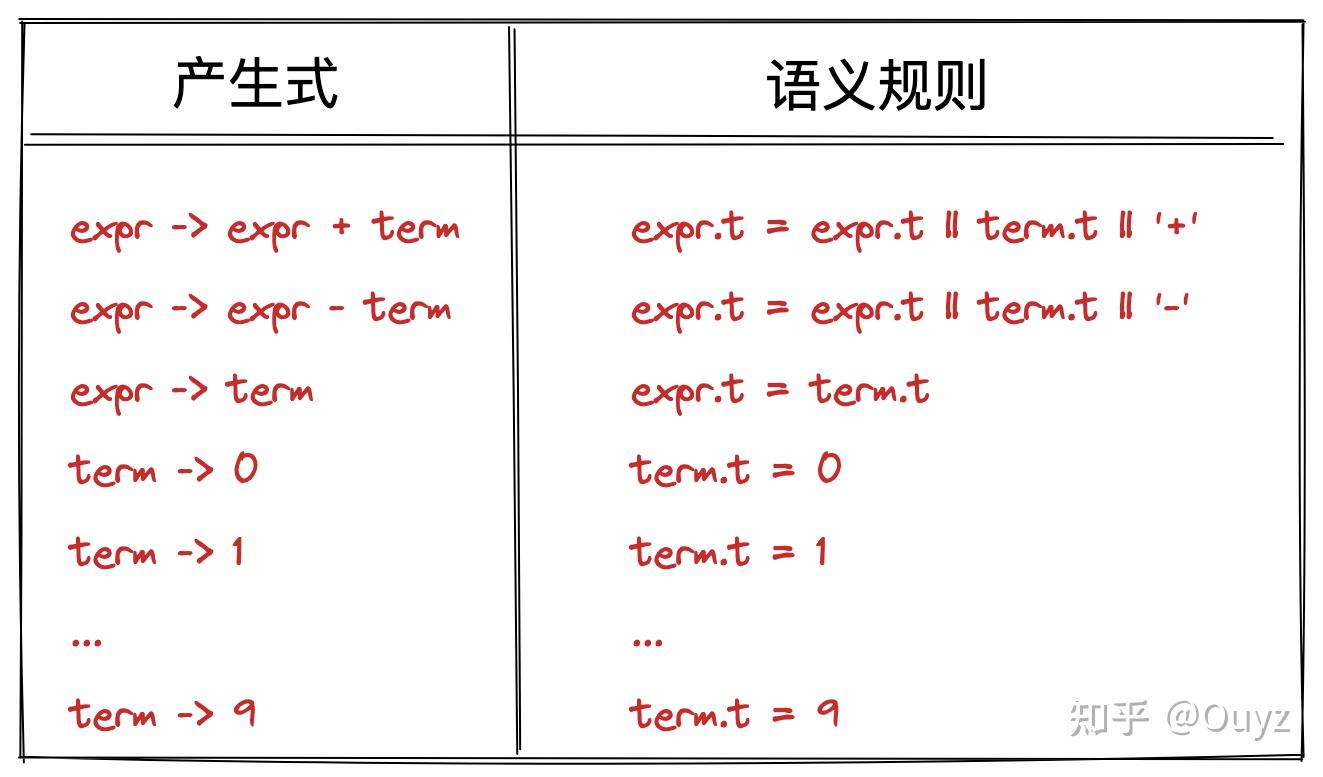

什么是语法制导翻译方案(SDT)
语法制导翻译方案是一种在文法产生式中附加一些程序片段来描述翻译结果的表示方法,这些程序判断称之为语义动作,语义动作按照惯例放在花括号中,写入产生式中。
具体的,我们还是以上面的中缀表达式翻译为后缀表达式的例子来理解,使用语义动作来达到属性计算同样的效果:
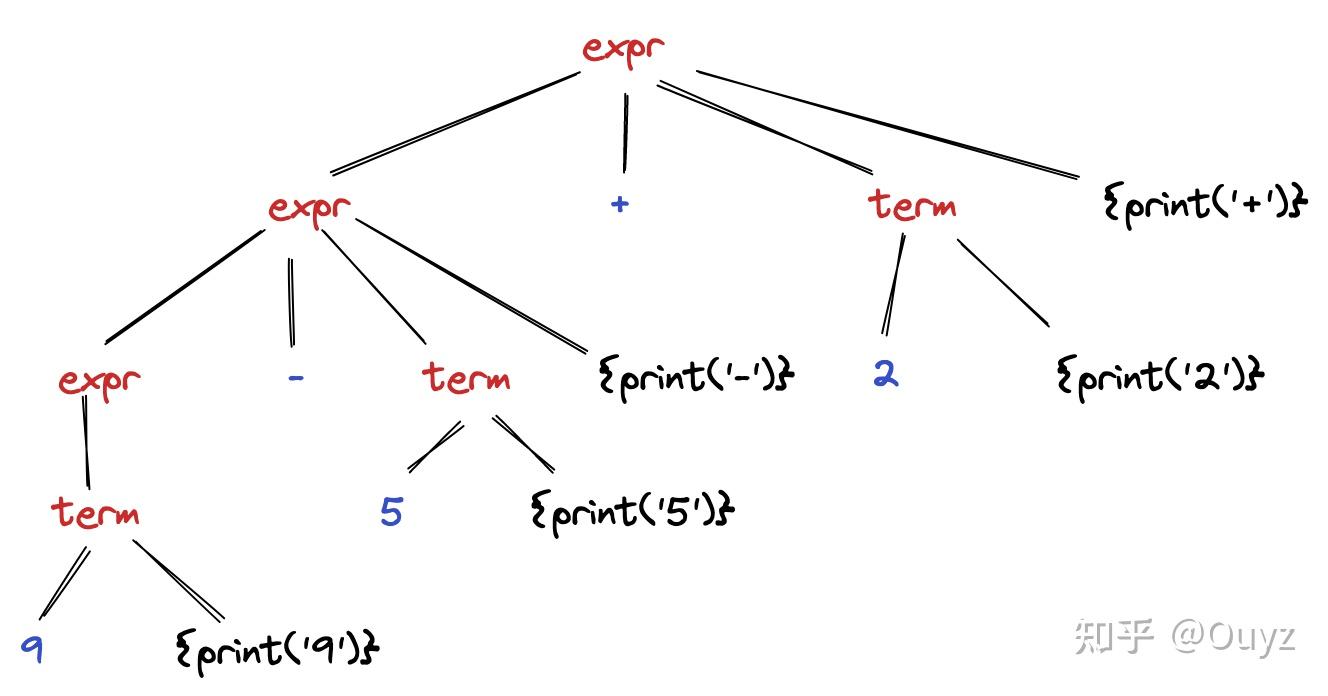

我们按照从左到右的深度优先遍历方式,并在我们访问它的叶子结点时执行相应的语义动作,那么执行结果就是翻译得到的后缀表式形式。
一个语义动作在产生式中的位置决定了这个动作的执行时间。当我们把语义动作放入产生式中后,得到:


语法分析
我们提过语法分析的基本任务就是:决定如何使用文法生成一个给定的终结符号串的过程。根据语法分析树结点的构造顺序,可以归为以下两类:
自顶向下分析方法
自顶向下的分析可以看成是从开始符号 推导出终结符号串
的过程。
输入中当前被扫描的终结符号通常称为「向前看(lookahead)符号」。
在每一步的推导中,都需要做两个选择:
- 替换当前产生式中的哪个非终结符号。
- 用该非终结符号的哪个候选式进行替换。
关于第一个选择通常面临两种策略:最左推导和最右推导。这里我补充一下哈工大陈鄞老师的编译原理公开课的讲解图,对两种推导过程的描述十分清晰:
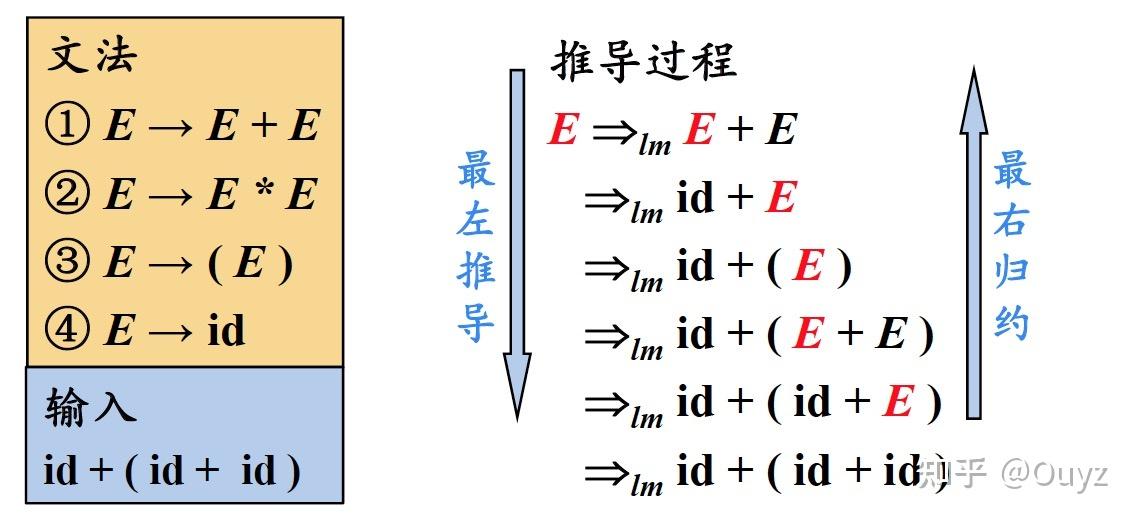

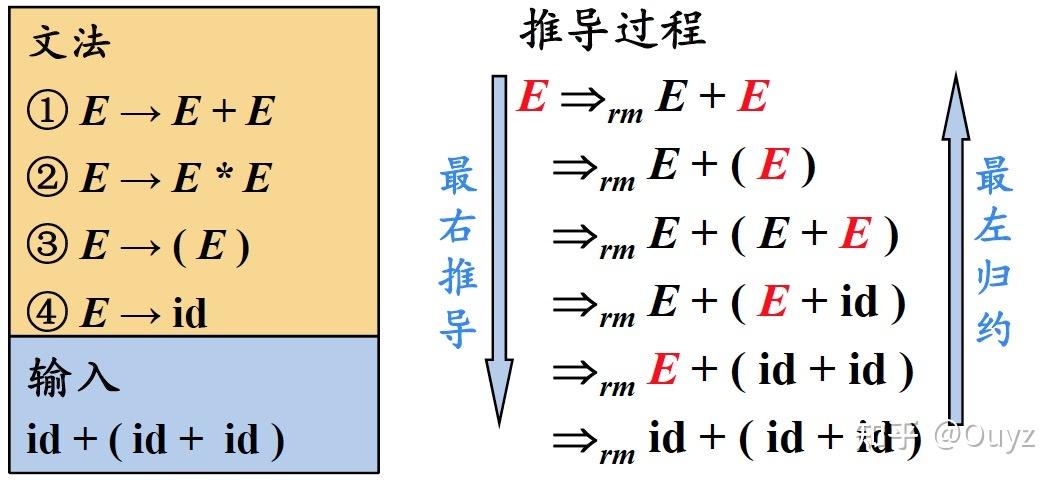

此外,我们通常将最右推导称为规范推导,这是因为在自底向上的分析中,编译器通常采用最左归约的方式(可以处理更多的文法和翻译方案),因此把最左归约称为「规范归约」,而最右推导相应地称为「规范推导」。
关于第二个选择,一般来说,为一个非终结符号选择产生式是一个“尝试并犯错”的过程。也就是说,我们首先选择一个产生式,并在这个产生式不合适时进行**回溯,**再尝试另一个产生式。一个产生式“不合适”是指使用了该产生式之后,我们无法构造得到一颗与当前输入串匹配的语法分析树。
预测分析法
在计算机对自顶向下分析的具体实现中,通常采用一种「递归下降分析(Recursive-Descent Parsing)」方法。它使用一组递归过程来处理输入,文法的每个非终结符号都有一个相关联的过程。
在这里我们考虑递归下降分析方法的一种简单形式,称为「预测分析法(Predictive Parsing)」。在预测分析法中,各个非终结符号对应的过程中的控制流可以由向前看符号无二义的确定。在分析输入串时出现的过程调用序列隐式地定义了该输入串的一颗语法分析树,当然,也可以通过这些过程调用显式的构造一颗语法分析树。
接下来,我们以一个精简版的文法生成 C 或 Java 语句的子集:
该文法精简忽略了 expr 和 other 非终结符号的产生式,如下是该文法对应的预测分析器伪代码片段:
void stmt() { switch( lookahead) { case **expr**: match(**expr**); match(';'); break; case **if**: match(**if**); match('('); match(expr); match(')'); stmt(); break; case **for**: match(for); match('('); optexpr(); match(';'); optexpr(); match(';'); optexpr(); match(')'); stmt(); break; case **other**: match(**other**); break; default: report("syntax error");void optexpr() { if(lookahead == **expr**) match(**expr**);}void match (terminal t) { if(lookahead== t) lookahead= nextTerminal; else report("syntax error");}其中,过程调用 match(t) 将它的参数 t 和向前看符号比较,如果匹配就进入下一个输入终结符号。因此,match 改变了全局变量 lookahead 的值,该变量存储了当前正在被扫描的输入终结符号。
FIRST 和 FOLLOW 集合
可以看到预测分析的控制流需要知道哪些符号可能成为一个产生体所生成串的第一个符号。由此,我们引入 FIRST 集概念:
FIRST 集定义
我们另 α 是一个文法符号(终结符号或非终结符号)串,将 FIRST(α) 定义为:
α 生成的一个或多个终结符号串的第一个符号的集合α 就是 ε 或者可以生成 ε , 那么 ε 也在FIRST(α) 中。例如在上面的文法中:
FOLLOW 集定义
此外,对于非终结符号 A,我们可以将 FOLLOW(A) 定义为:
$ 添加到FOLLOW(A) 中。例如在形式如 的推导中,FOLLOW 有如下形式定义:
关于计算 FIRST(α) 和 FOLLOW(A) 的算法的详细描述,我们在今后的文章中再继续深入。
左递归
递归下降分析法有可能陷入无限循环。当出现如下所示的“左递归”产生式时,分析器就会进入无限循环:
其原因是,产生式体的最左边的符号和产生式头部的非终结符号相同。假设 expr 对应的过程决定使用这个产生式,因为产生体开头是 expr,所以 expr 对应的过程将被无限调用。
通过改写有问题的产生式就可以消除最递归。考虑有两个产生式:
其中,非终结符号 A = expr,串 = + term,串
= term (即
),我们可以通过如下改写消除最递归:
得到的新的文法定义中,非终结符号 R 和它的产生式 是右递归的(right recursive),因为这个产生式的右部的最后一个符号就是 R 本身。
词法分析
词法分析器的主要任务就是从输入中读取字符,识别并将他们组成“词法单元对象”。词法单元(token)除了用于语法分析的终结符号之外,还包括一些附加信息,以属性值的形式出现。
构成一个词法单元的输入字符序列称为词素(lexem)。因此,我们可以说,词法分析器使得语法分析器不用考虑词法单元的词素表示方式。
若仅考虑一些简单的情况,我们可以将 token 的识别任务简单分为以下几种:


此外,在词法分析器的实现过程中,需要使用到以下两个技术:
- 剔除空白和注释:在词法分析阶段,通常在遇到空格、制表符或换行符时会跳过该空白部分,以简化语法分析器的设计。
- 预读:在决定向语法分析器返回哪个词法单元之前,词法分析器可能需要预读一些输入字符。一个通用的预先读取输入的方法是使用输入缓冲区。
符号表
符号表(symbol table)是一种供编译器用于保存有关源程序构造的各种信息的数据结构。这些信息在编译器的分析阶段逐步收集放入符号表,并在综合阶段用于生成目标代码。
符号表中的每个条目中包含一个与标识符相关的信息,比如它的字符序列(词素)、它的类型、它的存储位置和其他相关信息。
符号表条目是在分析阶段由词法分析器、语法分析器和语义分析器创建并使用的。但通常情况下,词法分析器一般不会建立符号表,只是向语法分析器返回一个词法单元,由语法分析器决定是使用已创建的符号表条目,还是为这个标识符新建一个条目。
实现符号表的通常数据结构,可以是:
符号表通常需要支持同一标识符在一个程序中的多重声明。我们可以为某个作用域建立一个单独的符号表,在这个块中每个声明都在此符号表中有一个对应的条目。
针对语句块的最近嵌套(most-closely)规则:一个标识符 x 在最近的 x 声明的作用域中,即从 x 出现的块开始,从内向外检查各个块时找到的第一个对 x 的声明。在实现上,我们可以将符号表链接起来,使得内嵌语句块的符号表可以指向外围语句块的符号表。
生成中间代码
我们前面的章节中提到过,两种最重要的中间表示形式是:
注意:语法分析树和语法树不是一种东西。通常,我们把前者叫做“具体语法树”,其能够体现推导的过程;后者叫做“抽象语法树”,其不体现过程,只关心最后的结果。
抽象语法树
在语法分析的过程,将创建抽象语法树的结点来表示有意义的程序构造。随着分析的进行,信息以结点相关的属性的形式被添加到这些节点。
在这里我们给出一个创建抽象语法树的翻译方案。
对于每一个的构造,我们可以用一个结点表示,其子结点代表此构造中具有于语义含义的组成部分。比如,在 C 语言的一个 while 语句
中,具有语义含义的部分是表达式 expr 和 stmt。因此,我们的 while 语句的抽象语法树结点有一个运算符,我们称为 while,并有两个子结点——分别是 expr 和 stmt 抽象语法树。
如下图,我们通过以下的翻译方案为一个有代表性但却很简单的由表达式和语句组成的语言构造出一颗语法树。其中,结点被实现为 Node 类的对象。类 Node 有两个直接子类 Expr(代表各种表达式)和 Stmt(代表各种语句)。每一个语句都有一个对应的 Stmt 的子类,如 while 语句对应子类 While,该类的构造函数参数对应抽象语法中的运算分量。
静态检查
静态检查是指编译过程中完成的一致性检查,包括:
三地址码
三地址码由类似于汇编语言的指令序列组成,每个指令最多包含三个操作数(operand)。我们可以看一下常见的三地址指令:
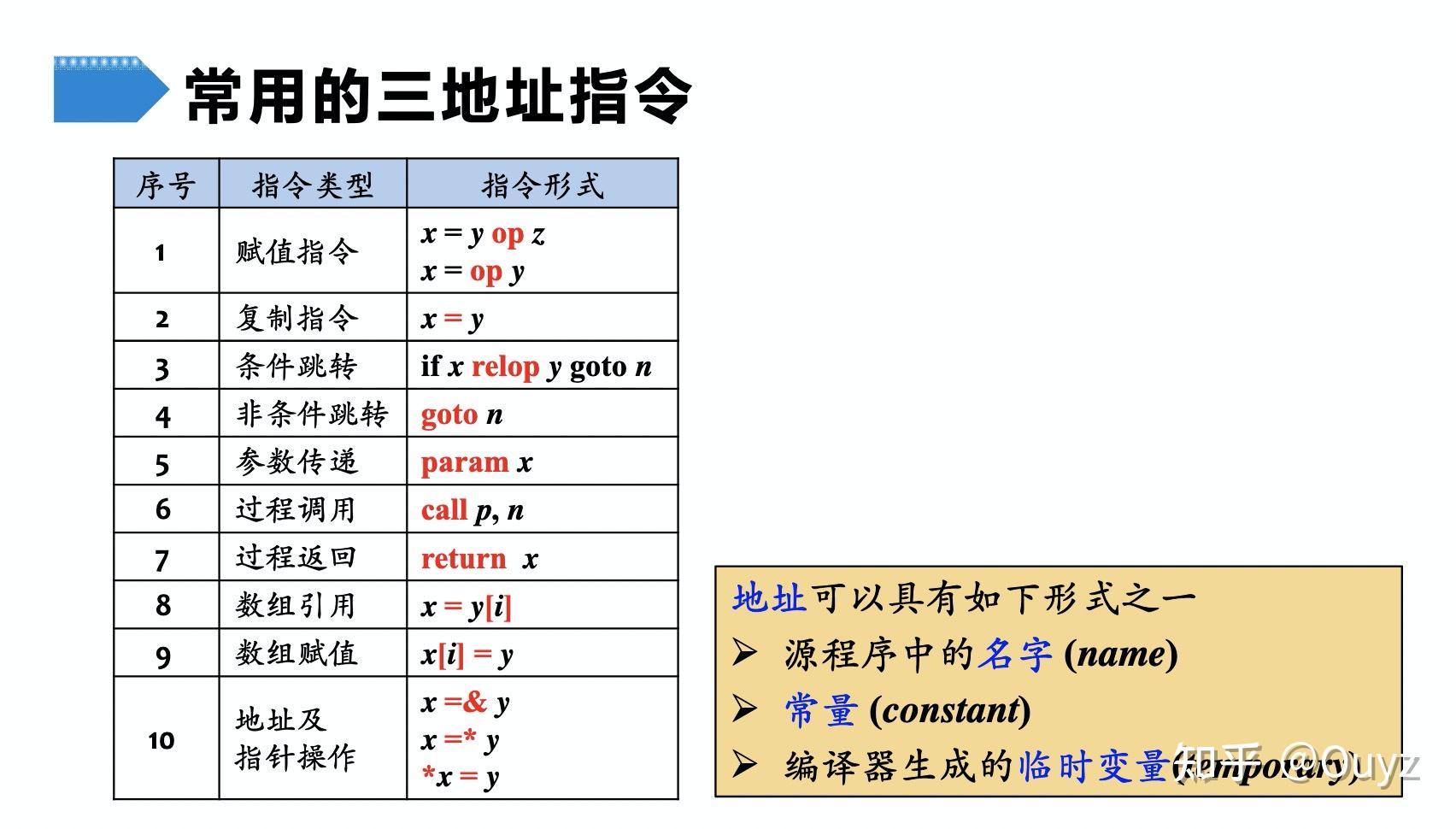

三地址指令将被顺序执行,但是当遇到一个条件或无条件跳转指令时,执行过程就会跳转。我们选择下面的指令来控制程序流:
ifFalse x goto L 如果 x 为假,下一步执行标号为 L 的指令ifTrue x goto L 如果 x 为真,下一步执行标号为 L 的指令goto L 下一步执行标号为 L 的指令在一个指令前加上前缀 L: 就表示将标号 L 附加到该指令上,同一个指令可以同时拥有多个标号。
接下来我们看看,在实现过程中如何利用抽象语法分析树来生成三地址码。
语句的翻译
我们以语句 的翻译为例,通过利用跳转指令来实现语句内部的控制流。如下,是 if 语句对应三地址码的代码布局:
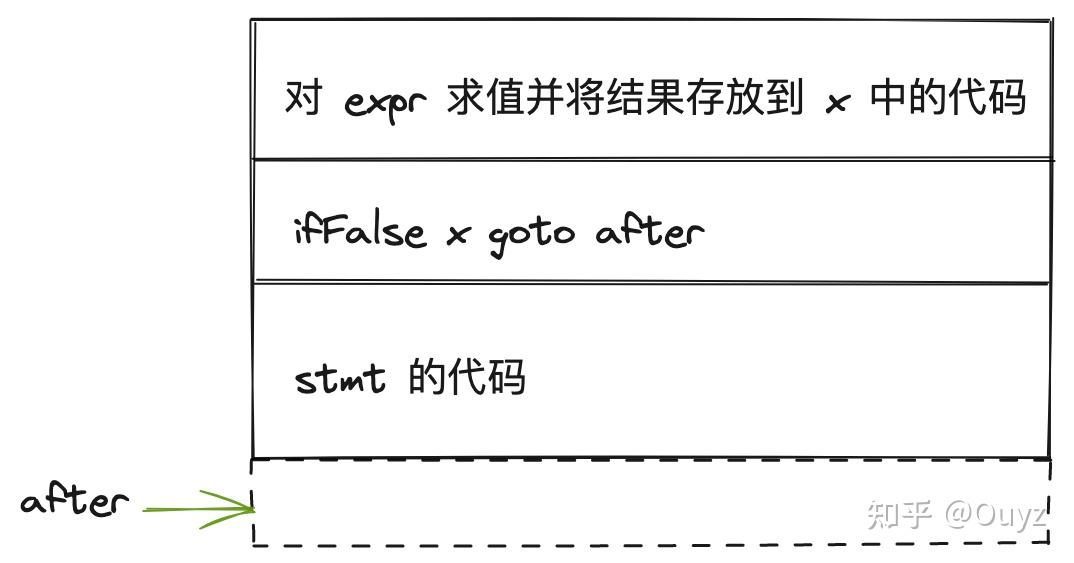

为具体说明,我们给出一个类 If 的伪代码实现(前面提过类 If 实现为 Stmt 的子类,其他语句都有对应的 Stmt 子类实现),包含一个构造函数以及生成三地址码的 gen 方法:
class If extends Stmt { Expr E; Stmt S; public If(Expr z, Stmt y) { E=x; S=y; after = newlabel(); } public void gen() { Expr n =E.rvalue(); emit("ifFalse" + n.toString() + "goto" + after); S.gen(); emit(after + ":"); }}其中:
- 构造函数有两个参数
x(表达式结点) 和y(语句结点),被存放在属性E和S中。同时,调用newlabel()給属性after赋予一个唯一的新的标号。 - 并有一个所有语句类都有的
gen方法。它调用E.rvalue()翻译表达式E,并保存E.rvalue()返回的结果结点。然后,gen方法生辰一个条件跳转指令,并且调用S.gen()来翻译子语句S。
表达式的翻译
我们将考虑包含二目运算符 op,数组访问和赋值运算,并包含常量和标识符的表达式,来说明对表达式的翻译。其中,要求数组访问 y[z] 中,y 必须是标识符(即支持 a[a[n]] ,但不支持 a[m][n])。
简单起见,我们为一个表达式的语法树中每一个运算符结点生成一个三地址指令。不需要为标识符和常量生成任何代码,它们可以作为地址出现在三地址码中。
因此,i - j + k 我们生成如下两个三地址码(生成临时变量保存中间结果):
t1 = i - jt2 = t1 + k但是,对于包含数组访问的表达式,我们无法简单的使用临时变量替换来生成我们想要的三地址指令。
这里我们用一个简单的方法,使用两个函数 lvalue(左值) 和 rvalue(右值) 来对表达式进行翻译。
在我们的简单语言中,表达式 x 出现在左部的只有两种情况:
x = 1 ,即 x 的类是 Id。a[i],结点 x 的形如 Access(y, z),y 是数组名称,z 是访问偏移量。相应的,lvalue 伪代码实现为:
Expr lvalue(x: Expr) { if( x是一个 Id 结点 )return z; else if( x是一个 Access(y, z) 结点,且 y 是一个 Id 结点){ return new Access(y, rvalue(z)); } else error;}相对而言,rvalue 实现会复杂一点,该函数返回一个(可能是新生成的)结点。此外,他需要考虑的 x 情形分为以下几种:
x 或 2,直接返回 x 本身。y op z,则代码先计算 y' = rvalue(y)及 z' = rvalue(z)。它创建一个新的临时名字 t 并产生指令 t = y' op z'(更精确地说,生成一个由 t、y'、op 和 z' 的字符串组合而成的指令字符串)。然后返回一个对应于标识符 t 的 Id 结点。y[z],我们可以复用函数 lvalue。函数调用lvalue(x)返回一个数组访问 y[z]'] 其中 z' 代表一个标识符,它保存了数组访问的偏移量。函数 rvalue 会创建一个临时变量 t,并按照t= y[z'] 生成一个指令,最后返回一个对应于 t的 Id 结点。y=z,那么代码将首先计算 z'= rvalue(z)。它生成一条计算 lvalue(y)=z' 的指令,并返回标识符结点 z'。rvalue 伪代码实现为:
Expr rvalue(x: Eapr) { if( x是一个 Id 或者 Constant 结点 ) return x; else if( x是一个 Op(op, y,z) 或者 Rel(op,y,2) 结点 ) { t = 新的临时名字; 生成对应于 t = rvalue(y) op rvalue(z) 的指令串; return 一个代表 t 的新结点; } else if ( x是一个 Access(y,z) 结点 ) { t=新的临时名字; 调用 lvalue(z),它返回一个 Access(y,z') 的结点; 生成对应于 t = Access(y,z') 的指令串; return 一个代表 t 的新结点; } else if( x是一个 Assign(y,z) 结点 ){ z'= rvalue(z); 生成对应于 lvalue(y)= z' 的指令串; return z; }}可以通过下面这个例子来看表达式翻译的效果:
a[i] = 2 * a[j-k]# 将生成如下三地址码t3 = j - kt2 = a [ t3 ]t1 = 2 * t2a [ i ] = t1总结
到目前为止,我们大致介绍了语法制导翻译涉及到的相关过程和技术,有些地方本人理解可能有误,欢迎大家留言交流或帮忙指正。
在接下来的章节中,我们会利用学到的知识构造一个简单的语法制导翻译器。
















如果认为本文对您有所帮助请赞助本站