投射模。设是-模,对于任意满同态和同态,总有同态使得下图交换.如果对任意单同态和同态,总有同态使...

投射模。设 是
-模,对于任意满同态
和同态
,总有同态
使得下图交换.
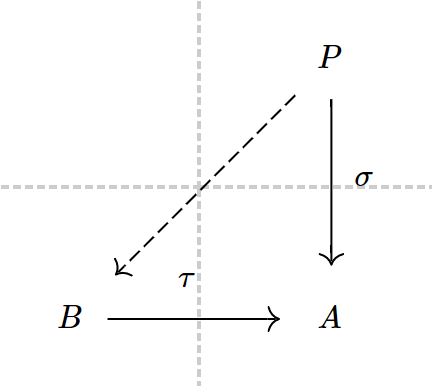

如果对任意单同态 和同态
,总有同态
使得下图交换,称
为内射模。
对于 ,如果
的非零子模与
相交,称
为
的本性扩模。
引理, 是内射模当且仅当
没有非平凡本性扩模。
内射包是内射的本性扩模,意即最小的内射扩模。内射包在同构意义下唯一存在。
投射盖。设 是投射模,
是满同态,如果对于任意投射模
与满同态
,使得
的
总是满同态,那么称
是
的投射盖。
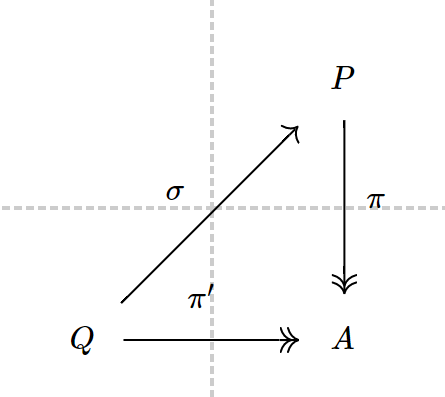

投射盖在同构范围内唯一。但是投射盖并不总存在。
自反模与半自反模。对于左 -模,
是右
-模,记为
.当
时,称为自反模,当
称为半自反模,或缺扰模。
对于 ,以下的
分别叫作推出与拉回:
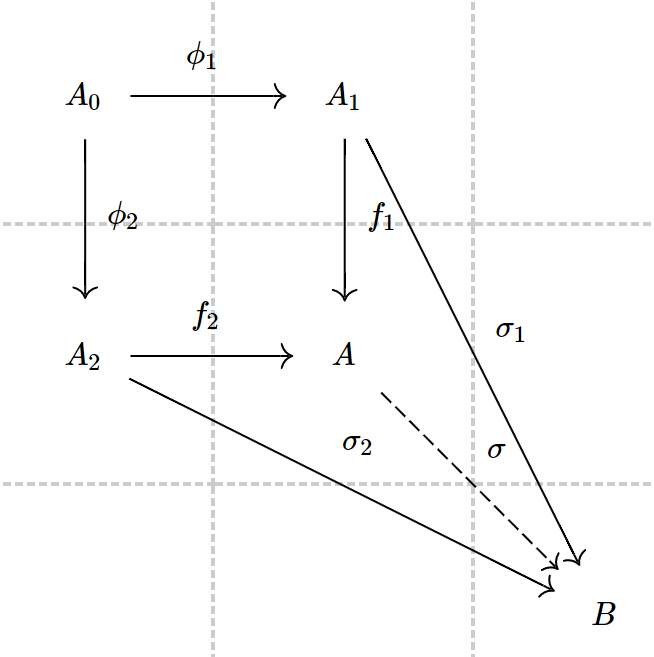

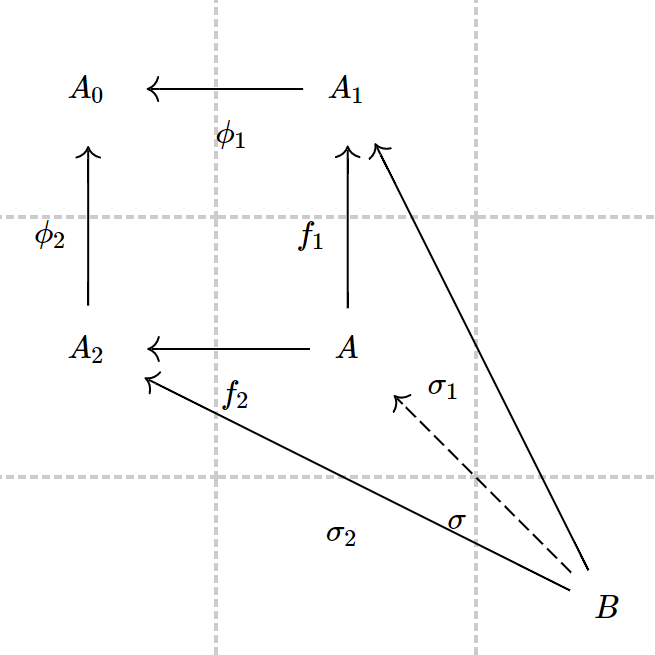

或者,以下的定义等价:
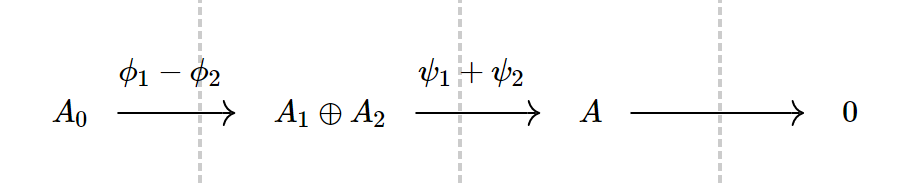
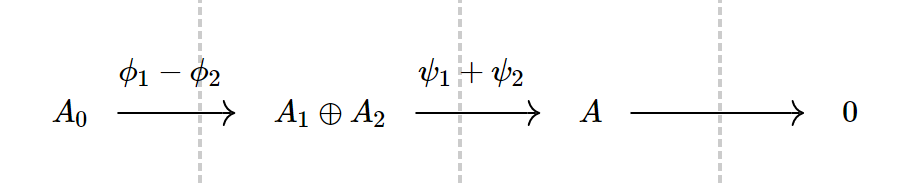
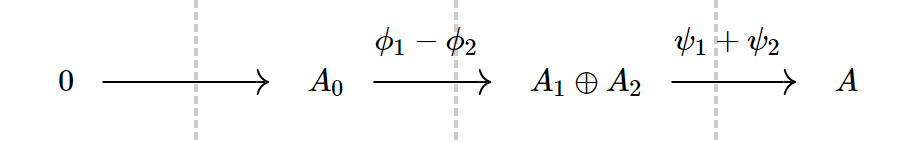
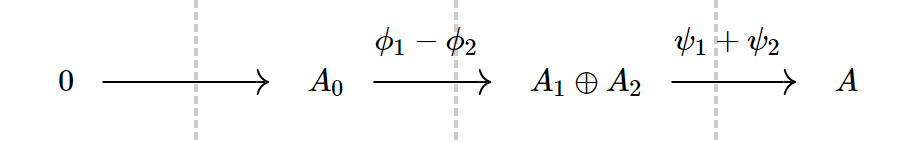
复形与微分。对于 ,如果
,称链为复形,
为微分。称
为其同调。
同调正合列定理。设 分别是复形,并且有正合列
使得如下图交换:
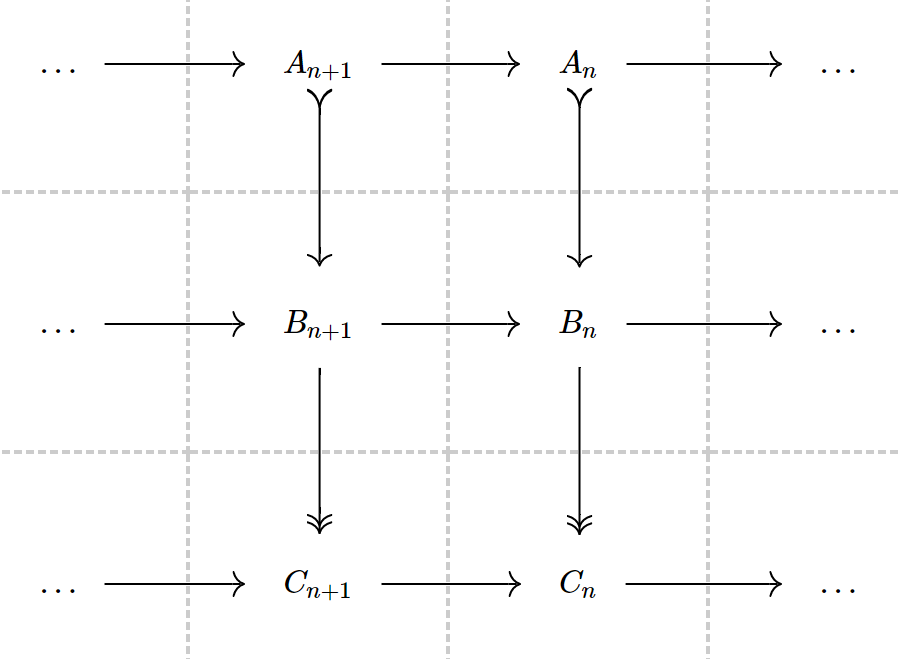

此时有 使得如下列正合:


的一个投射分解是一个由投射模构成的正合列:
.
箭头方向相反,将投射模改为内射模时,叫作内射分解。
核与上核。设 . 对于任意
,
与
使下图交换。
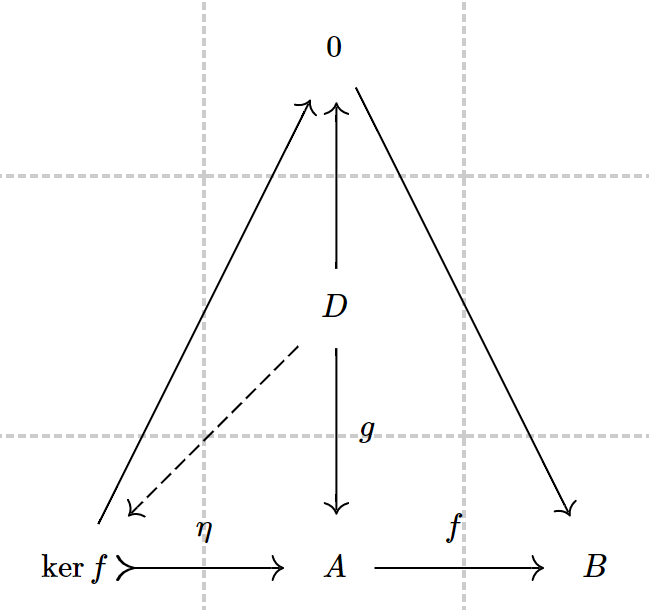

核的对偶概念是上核。
设 是
-模,
是共变加法函子。取
的投射分解为
,那么对其进行
的变换可得
,记
. 这个定义不依据
的选取而改变,因此
是
的共变函子。
将投射分解改为内射分解,得到的是 .
设 是自由模,生成元为
,那么对于任意
与
,只需要选取一组使得
使得
,并定义
即可得到
,因此自由模总是投射模。
对于任意的模 ,自然有自由模
使得
. 这给出了正合列
. 记
,重复这样的操作,就得到了:
此时,考虑它们的复合
经过化简,得到正合列
这说明任意模总有投射分解。
反之,任意模总可以嵌入某个内射模。首先注意到 模都是
内射模。假定
是
模,
而
. 假设有
是
的扩张,任取
,如果
,则规定
,否则规定
. 这样,根据佐恩引理,就得到了
. 对于一般的
,有嵌入
,具体地说,
. 已经知道
是
内射模,只需要证明
是
内射模。设有
和
. 对于每个
,
,而
,因此根据内射模的性质存在
. 对于每个
,定义
,那么
,并且
扩张了
.
如果 是正合列而
是内射模,类似地,考虑:
由此得到内射分解
.
设 是right
-module chain complex,它们之间的morphism
是一族
-module homormopshim,使得下图交换。
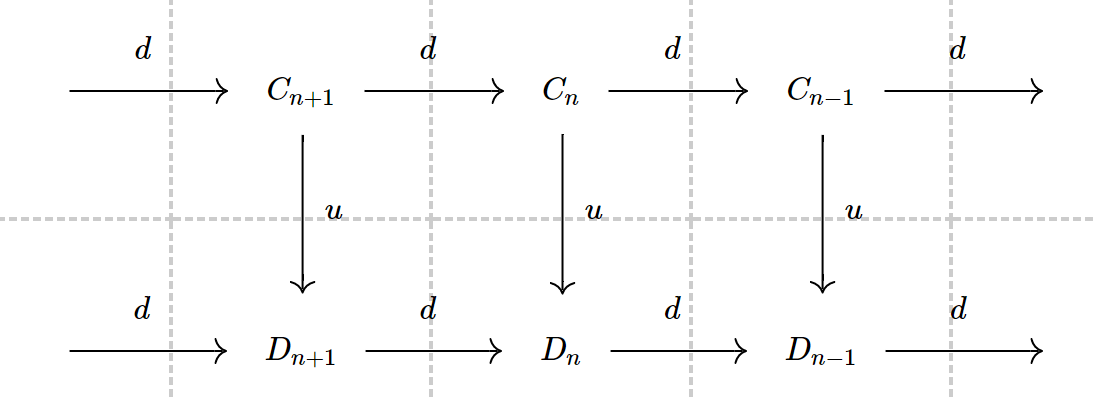

蛇引理:设有如下的交换图,且每行exact,那么有 的同态,并且
exact.
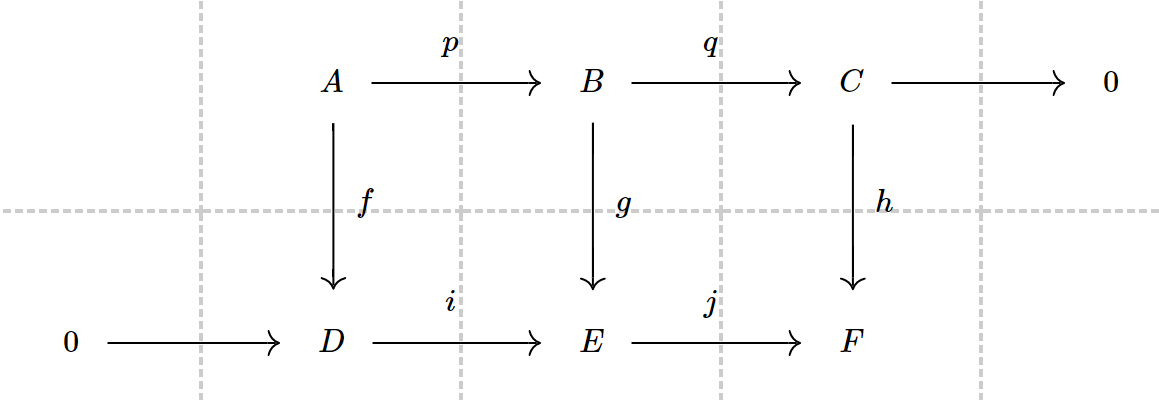

此外,当 是单射时,
也是单射;当
是满射时,
也是满射。
设 ,由于
是满射,所以存在
使得
,因此
,因为
,因此存在
使得
,令
. 换言之,
.
验证定义的良好性:假设 ,那么存在
使得
,因而
,这说明
.
五引理:设有如下的交换图,其中两行分别正合:
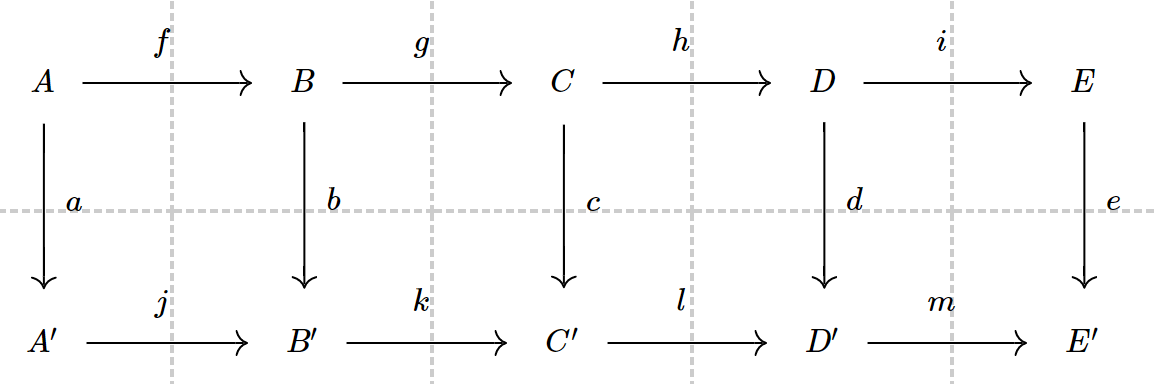

当 单射
满射时,
单射;当
满射
单射时,
满射;因此,
是同构时,
也是同构。
任取 ,那么
,因此
,记
,此时
,因此
,记
. 因为
是单射,所以
,而
.
反之类似。
对于chain complex ,记
,
,
,
. 考虑下图。
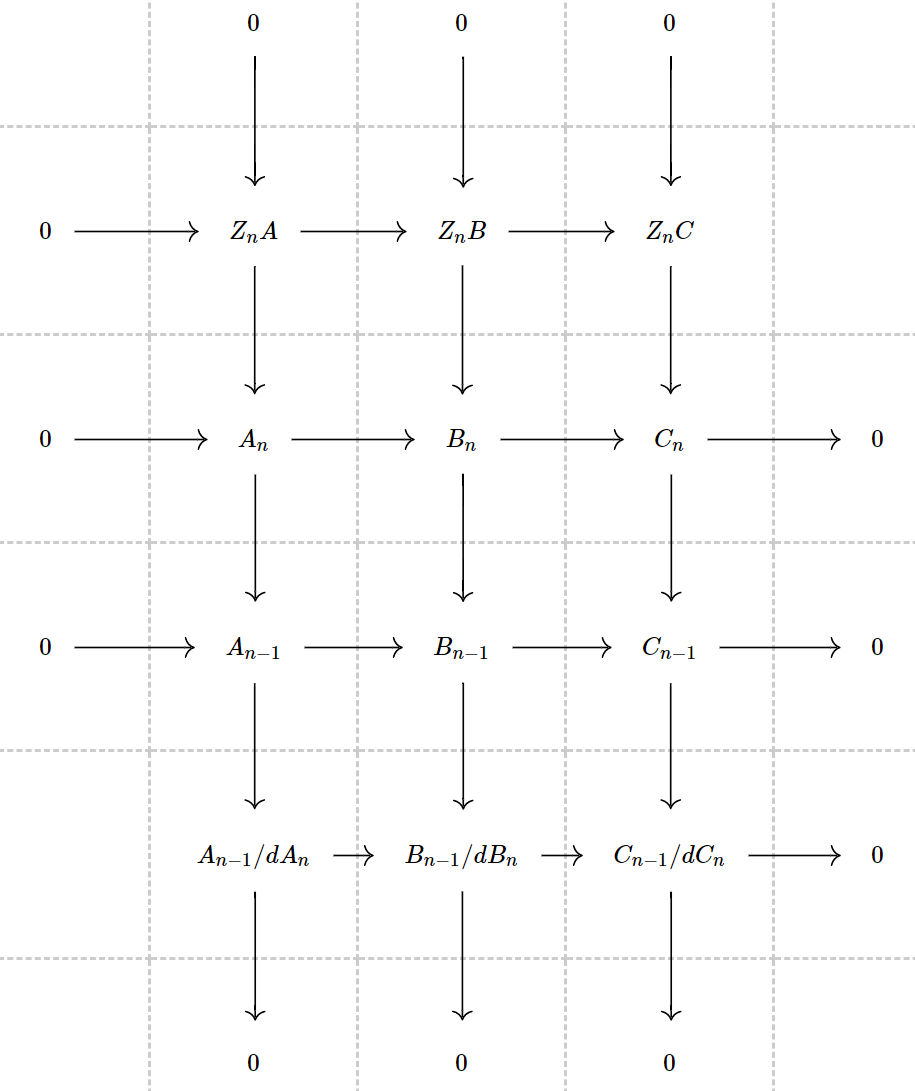

由于图的中间两行是正合的,所以根据蛇引理,每一行都正合且交换。
再注意到,对于 ,
,因此
,从而
给出了
的同态,并且下图正合交换:
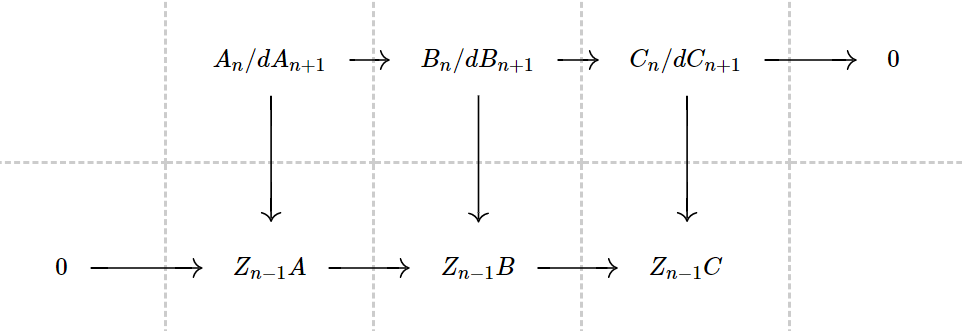

每一列的kernel是 ,而coker是
.因此,得到了正合列
.
对于线性空间范畴,chain complex可以视作 ,此时
可以视作映射
,如果记
,那么
将
映射为
,这说明
.
设有 ,此时定义
则
是
的态射。此时,
,因此
是chain complex的态射。
对于 ,如果存在上述
使得
,那么称
null homotopic,一个chain complex是split exact的当且仅当它的id映射null homotopic.
对于 ,如果
null homotopic,称对应的
是
与
的chain homotopy.
引理,设 null homotopic,则
是零态射。
设 是chain complex map,定义mapping cone是
,mapping cylinder是
,它们的微分映射分别是
和
.
设 是拓扑空间,
是它的所有开集构成的偏序集(大→小),
是阿贝尔范畴,由
到
的函子
如果满足
则称为一个presheaf. 进一步地,设
是开集
的开覆盖,
是一族元素,再设对于任意
,
与
经由态射
和
变换的结果相同,此时如果总有唯一的
使得它在态射
变换下恰等于
,那么称这个presheaf是sheaf.
sheaf的一个例子是这样的: ,后者有交换群结构所以是阿贝尔范畴,而
是函数的限制。假如
覆盖了
,对于每一个
,取
并定义
,那么定义是良好的并且
在
处连续。
的唯一性显然。
















如果认为本文对您有所帮助请赞助本站