在开始提出问题前,我们先回顾一下长度收缩公式的推导.

设有两个观察者分别静止于惯性参考系 和 中,S’系以速度 相对 系沿 轴运动.一细棒静止于 系中并沿 轴放置,如图14-6 所示. 系中观察者若测得棒两端点的坐标为 和 ,则棒长为 .通常把观察者相对棒静止时所测得的棒长度称为棒的固有长度 ,在此处 而 系中的观察者则认为棒相对 系运动,并同时( )测得其两端点的坐标为 和 ,则棒在 系中的长度为 .利用洛伦兹变换式,有 式中 .将上两式相减,得 即

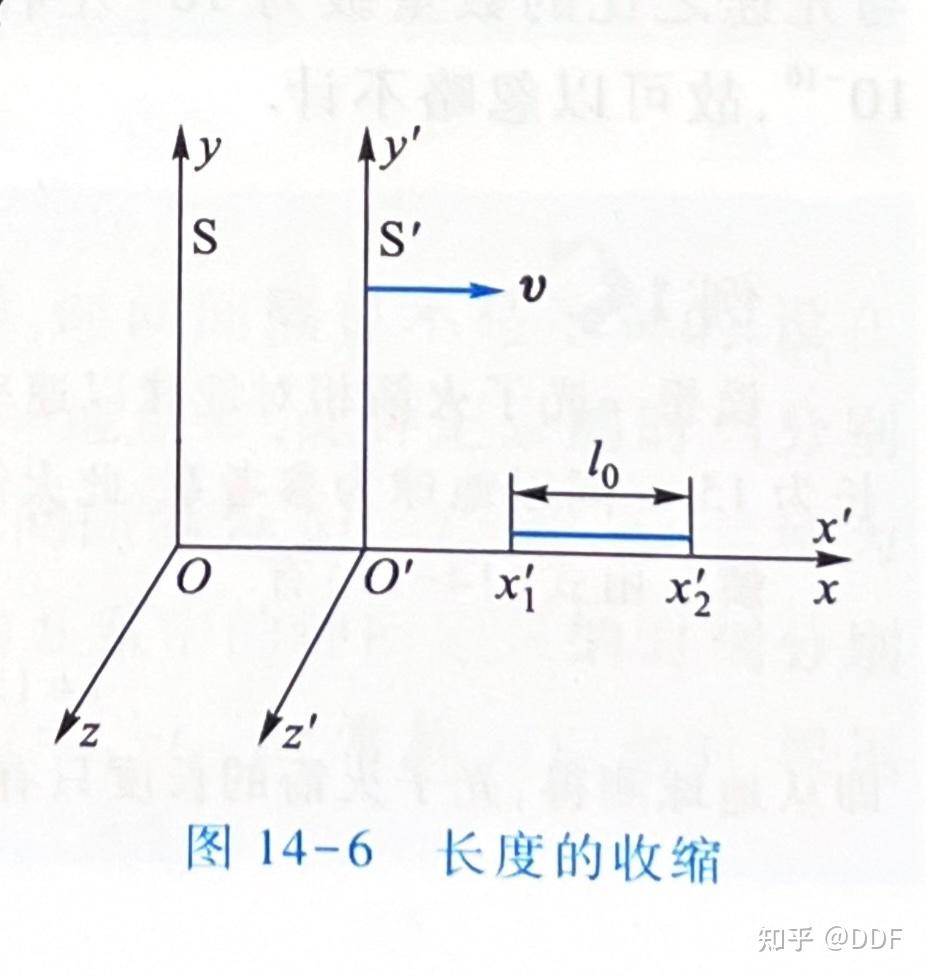
规定在 系中同时(即 )测量棒的长度,而在测量固有长度时,两次测量的时间间隔则不作规定.

---

上面的证明使用的公式是 ,式中 ,可直接推出长度收缩关系.课堂上我们老师留了一道思考题:用公式 来推导长度收缩公式.

在用公式 推导时,会遇到 的问题.此时,显然可以利用时空相对性(即公式 )把 转换成 和 ,再化简来求得同样的结果.

---

接下来老师提出的极具迷惑性的问题则是:既然在 系中两次测量时间间隔可取任意值,那我可不可以令其为 ?

于是,按照题设,我们可得 代入 ,求出 即 .

不难发现,这里求出的公式与长度收缩的公式正好相反.即

用 公式并规定 可得出 ;

用 公式并取 可得出 .

两式显然不等,那么问题出在哪里?

---

一位同学分享了他的思考:将 和 代入到 中,则分式为 ,为使分子为 ,则 ,则变为低速情况,且用 和 都能得到 .

我的反驳是:尽管在他的说法下用 和 都能得到 ，但一个是 一个是 ,在数学上不正确.

老师的说法是:本来 系的速度 接近光速 ,在他的说法下直接变成低速,是不正确的.

---

那么如何正确解决这个问题呢?我的回答如下:(已获老师认同)

问题中实际上提到了三个时间间隔,分别是在 系测量所取的 、在 系测量所取的 和由于时空相对性计算出的 .

虽然有两个量都用了 ,但它们的物理意义并不同.把它们混淆并混用，才产生了上面的矛盾.

在 系测量所取的 的物理意义显然,可以得到该 与由于时空相对性计算出的 在 时的 没有任何关系.

既然两者没有关系，那就既然两者没有关系，那就不能把 代入 去求两个长度的关系.

也正因为两者没有关系,才会出现代到 使得出现高速变成低速的矛盾.

---

总结:

该问题对于已经学过相对论长度收缩的读者可能是没有难度的、显而易见的,但对于初学者来说，可以作为一个很好的例子去理解长度收缩公式推导过程中的各个量.

参考:

1.东南大学等七所工科院校 编，马文蔚，周雨青，解希顺 改编.物理学（第七版）下册.北京:高等教育出版社，2021:293-294