趣味杂谈35：定量分析“登高望远”

编者按：高考之外，别有洞天！

有诗曰“欲穷千里目，更上一层楼”，

也有诗曰“独上高楼，望尽天涯路”，

那么，我们来定量分析一下，“登多高，望多远”的问题。

这里稍微涉及一些“等价无穷小量”的问题，

这里简单介绍一下，我在其他的很多文章中，也有过一些介绍，附在本文后面，感兴趣的小伙伴们可以自己浏览学习。

当 时，存在，

1. ，

2. ,

3. 。

上面这些相对比较常用，另外还有， ， 等等，

这些在大学时，学习高数的第一周或许就能学到了，

整体上看这些式子，大部分是“ ”，其中“ ”是“ ”，还有个更厉害的是“ ”，

我们不深究，只是“拿来主义”稍微运用一下而已哈!

然后，我们用这些知识点定量分析一下“登高望远”这件事情。

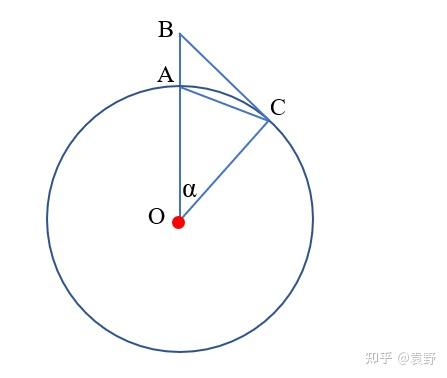
如上图，圆心为 的圆表示地球 ，地球上一楼高 ，在楼顶 点能看到 处，则 为圆的切线，即 ，已知地球半径 ， ，

因为 ，所以弧长 等于线段 长度，记为 表示了“登高望远”中的“望多远”的距离，

同时因为 ， 就是一个小量， ，就可以用到上面这些等价小量公式了，

首先，我们得到，

(1)

然后在 中，

(2)

根据等价无穷小量公式， ，得到，

(3)

将(2)式代入(3)式，得到，

(4)

将(4)式代入(1)式，得到，

，

因为，所以 ，从而将上式中根号内的分子分母同时除以 ，化解得到，

，

这样，我们就定量分析得到了“登高望远”问题的公式了。

这些知识点看起来和物理似乎关系不大哈，算了，就这样吧，好歹有个地球。下面附一些链接，其中也涉及到一些等价小量问题，和高考物理关系更加密切一些，

1.袁野：再讲一讲等价无穷小在单摆中的运用

2.袁野：简谐振动杂谈

3.袁野：趣味杂谈34：用平抛运动的方法推导匀速圆周运动的向心加速度公式

好了，就讲这些吧，小伙伴们，咱们下期再见啦！

更多精彩尽在“袁氏物语”！