萨迪·卡诺(SadiCarnot)在1824年设计了一个假想中的理想热机,在基于可逆过程的条件下做到了之间效率最高的变...

萨迪·卡诺 (Sadi Carnot) 在1824年设计了一个假想中的理想热机,在基于可逆过程的条件下做到了 之间效率最高的变换。
回忆一下热平衡和可逆过程
因为要保证可逆,
我们这里用另一种方式备注一下可逆过程:
可逆过程会保持热平衡不变以及不改变熵值
关于这句话的理解我们会慢慢体会到。这里我们只用理解通过上面两条,我们的卡诺循环 (The Carnot Cycle) 必须是由恒温和绝热过程组成的。
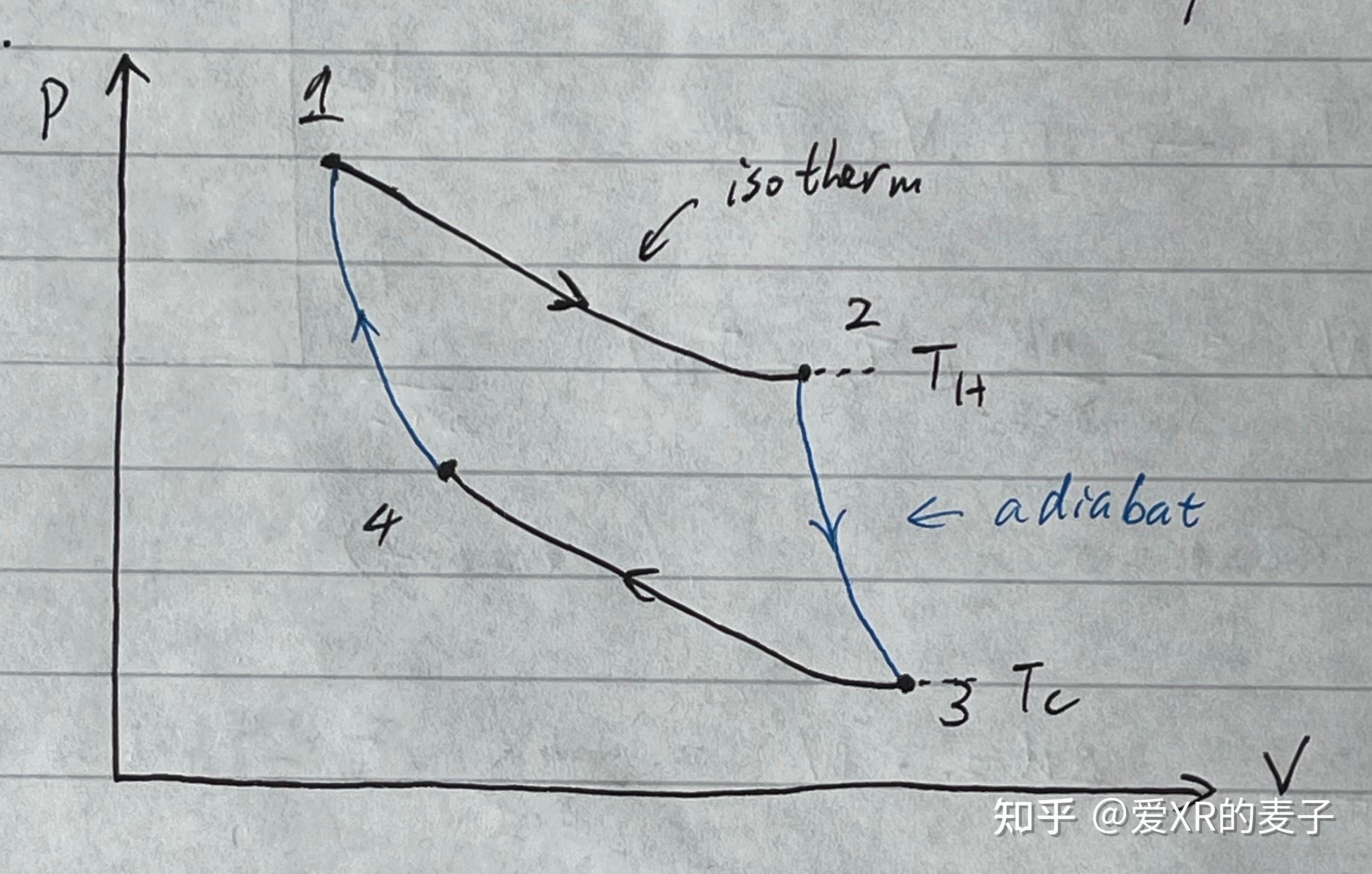

从压力-体积图的图像中,我们能看出来总做功是循环包围的面积。
通过考虑理想气体,我们还可以将值量化地算出来。
恒温膨胀
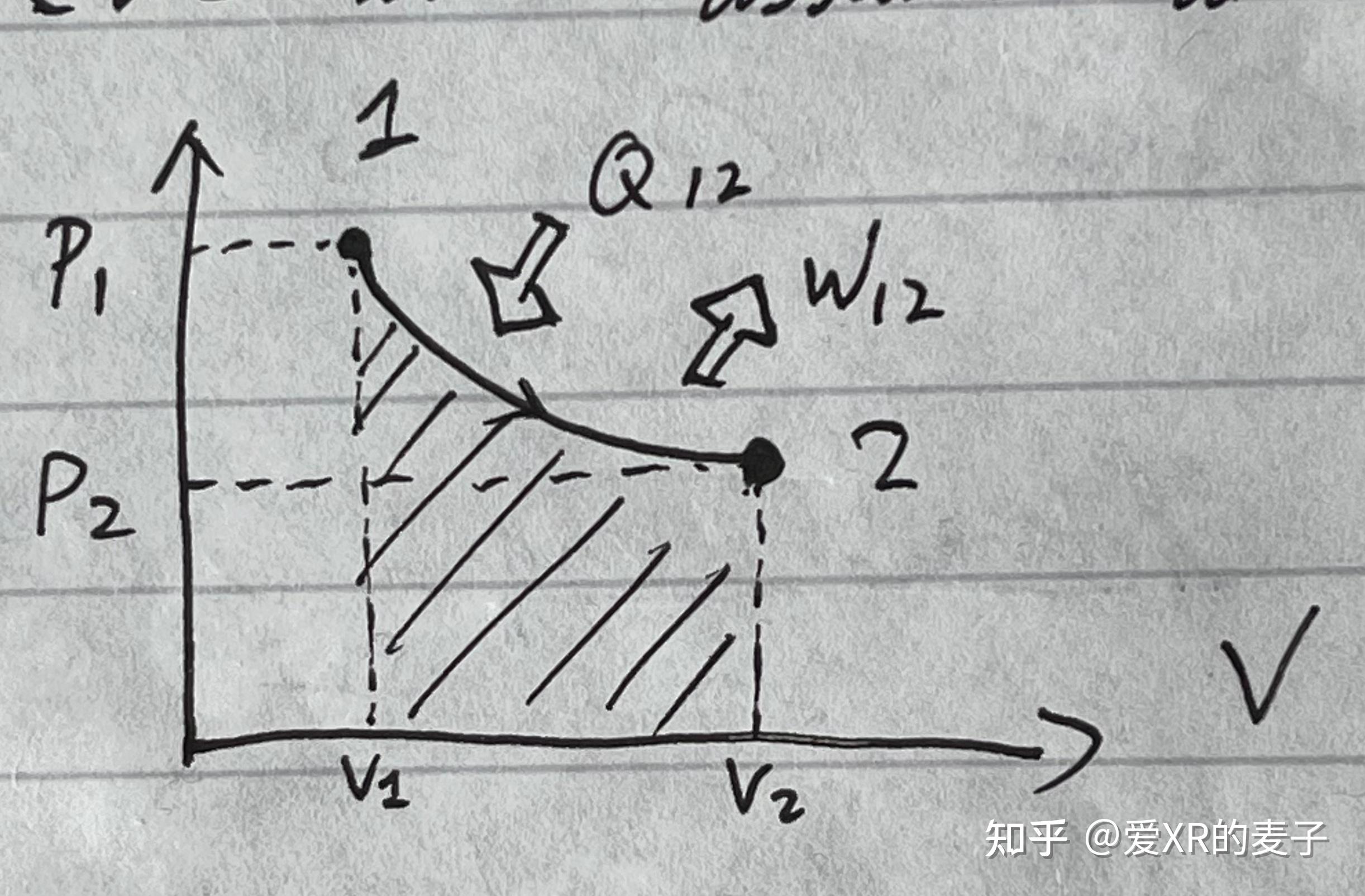

物态从 到
。
做功:
内能:
热量:
绝热膨胀
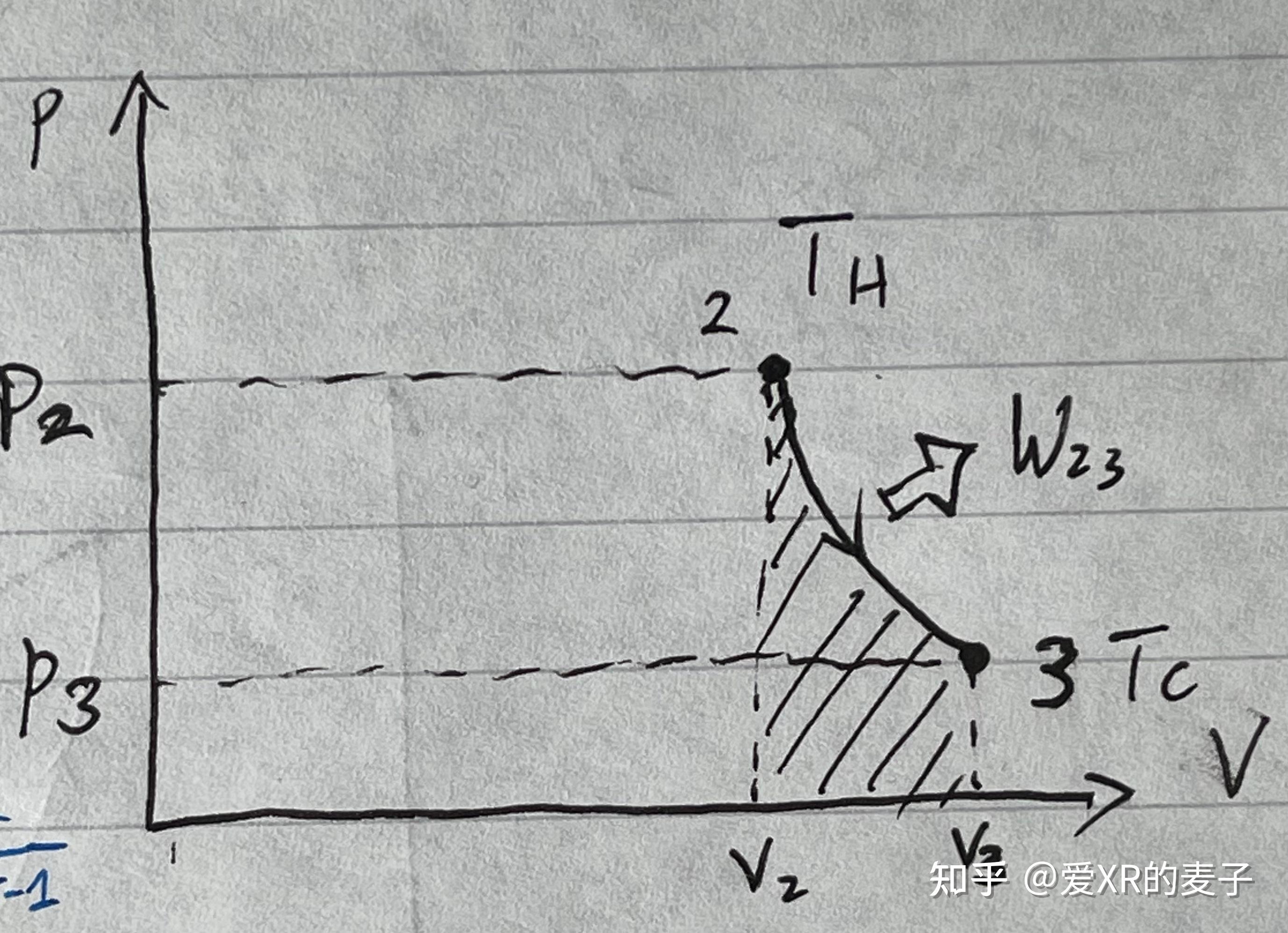

物态从 到
。
做功:
热量:
内能:
恒温收缩
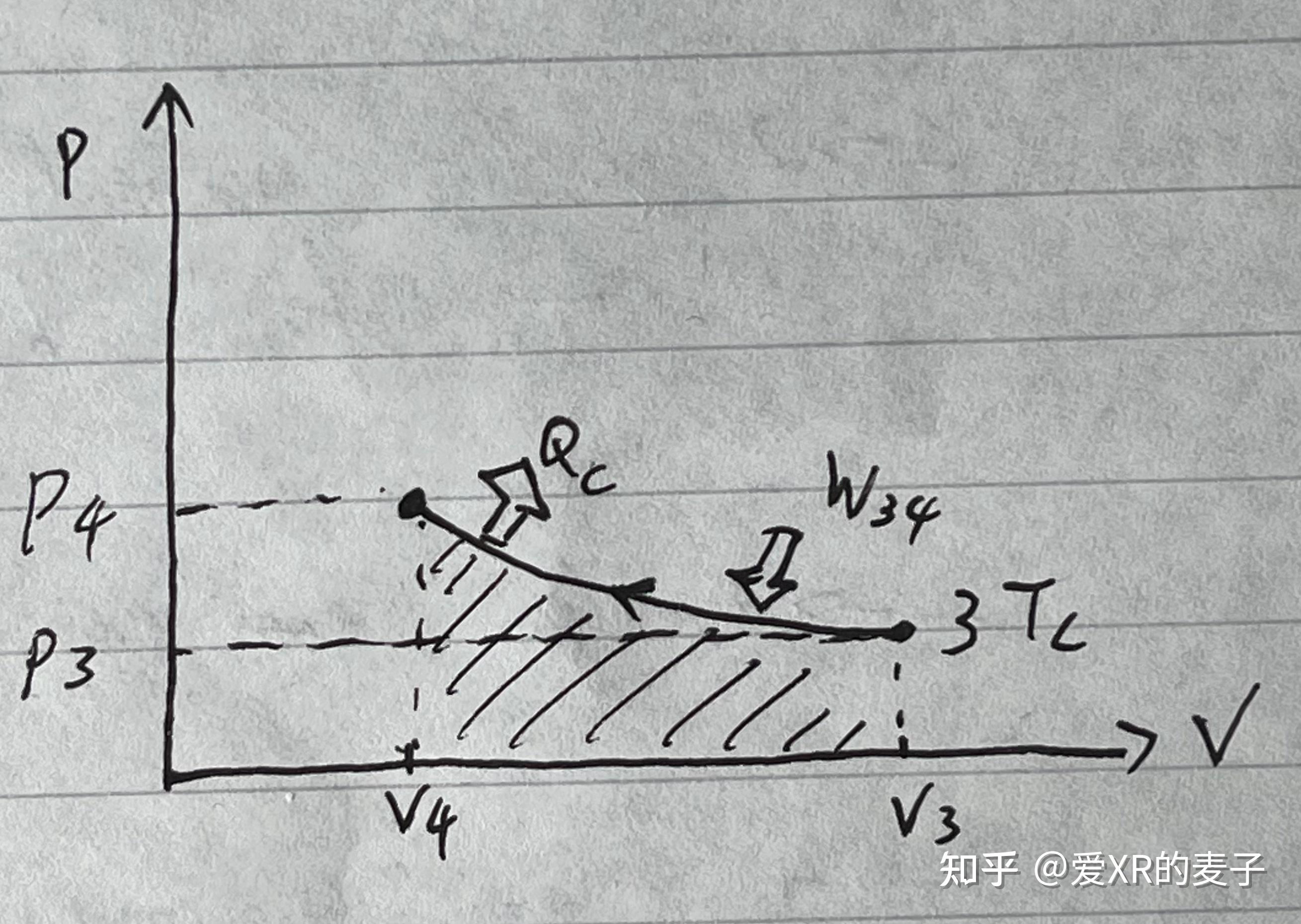

物态从 到
。
做功:
内能:
热量:
绝热收缩
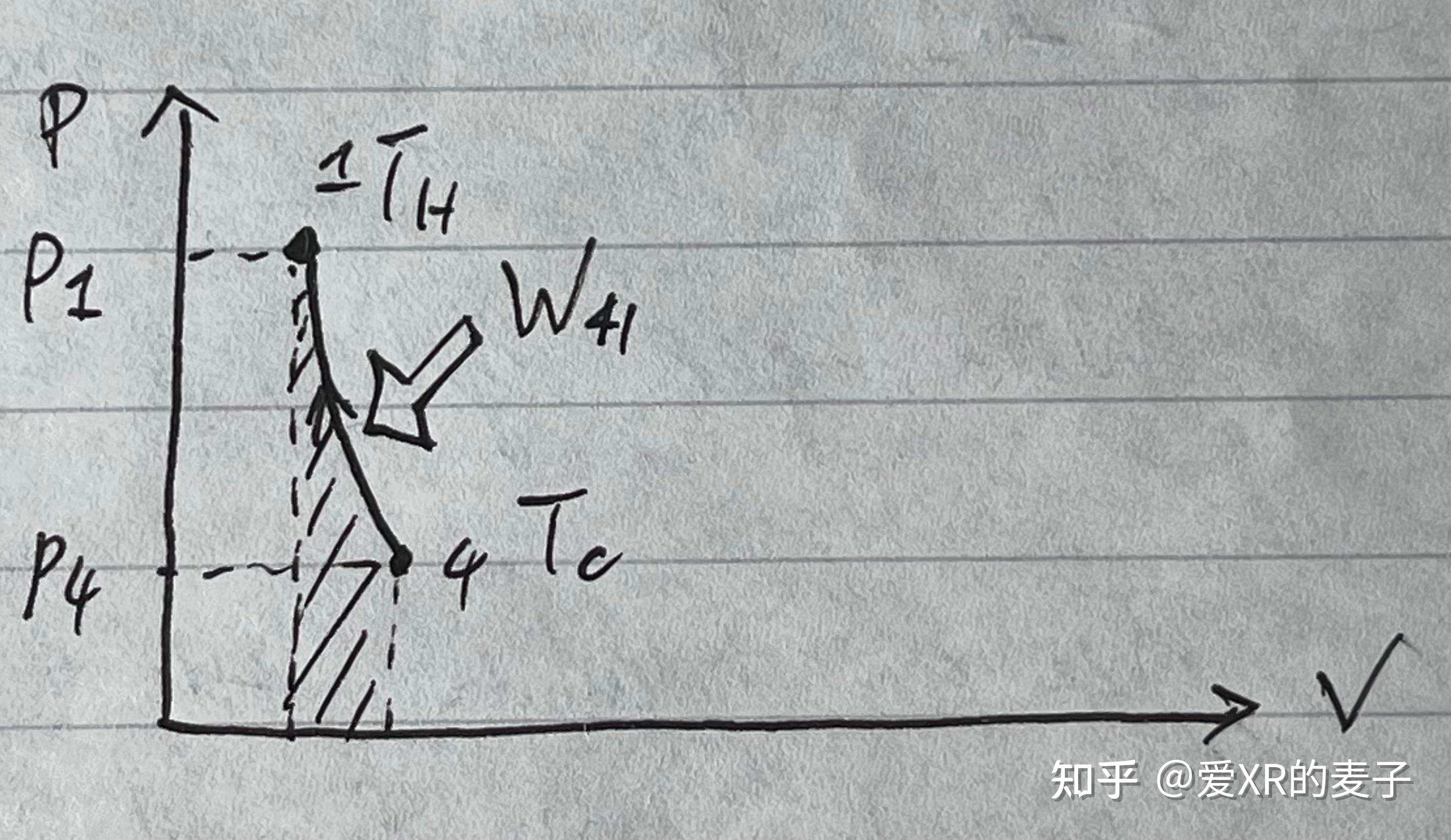

物态从 到
。
做功:
热量:
内能:
将所有内能变化加起来
而总的做功也就等于总的热量。
通过两段绝热过程,我们可以得到一个有用的关系式
有了它我们就可以得到做功的值了,先算下热量值
而做功为
我们也知道
卡诺引擎的效率
谈论卡诺引擎的效率前,我们先来给效率一个定义
而对于我们之前说的卡诺循环而言
而上面我们也对热量做过计算,代进来就好
再次利用
由此看来,对于卡诺引擎而言,其效率只取决于两个热库之间的温差。
我们也能从中看出当 时,
。但是
是一件不可能的事,这是热力学第三定律,下一篇会着重讲一讲。
卡诺循环在现实中生活中并不存在,最接近于卡诺循环的生活案例就是飓风现象了。我们之后会看到在两个温度之间,卡诺循环是效率最高的引擎系统了。一切人造系统的效率都将小于卡诺循环的效率。
开尔文温度温标 (Kelvin Thermodynamic Temperature Scale)
我们在之前就介绍了开尔文温标以及它与理想气体公式的关联。这里是另一个视角。当我们考虑卡诺引擎在两个温度之间传递热量时,我们需要测量相对于一个参考温度 , ,的温度,
,这时,
可以看出,这是一个线性的等比例关系,而且只需要一个参照点。(可以对比一下摄氏度来理解)
而卡尔文温标则是
卡诺制冷机 (The Carnot Refrigerator)
循环有一个有趣的做法。上面提到的卡诺引擎的卡诺循环 ( ) 是从外界吸热,气体做功。而如果整个循环反过来跑 (
) 则就是外界做功,气体吸热了。这样我们就可以从一个温度低的热库 (也就是我们的制冷机部分)吸取热量给到温度高的热库。


通过之前对热力第二定律的了解,想必你也知道,这个过程是必须做功的。
这里我们仿造效率再定义一个值,即制冷机的表现系数 (Coefficient of Performance)
这个反过来的卡诺循环,如果我们考虑温度低的热库所得到的就是制冷机。反过来,如果我们考虑的是温度高的热库,我们就得到了一个热泵 (Heat Pump)。我们同样可以得到热泵的表现系数
以上的所有讨论都是建立在理想上的可逆过程,那么真实的引擎与我们理想的情况到底差多远?
真实的引擎
那么学习卡诺循环的意义只在于一个理想上限吗?其实也不止于此,任何可逆过程都可以被看作很多个卡诺循环组成,而具体数量不限。(之后会看一些其他引擎,例如奥托循环)
卡诺定理 (Carnot's Theorem)
所谓的卡诺定理就是我们之前看到的一个称述
在两个温度之间,卡诺循环是效率最高的引擎系统了为了证明这个定理,我们可以使用反证法 (Proof By Contradiction)
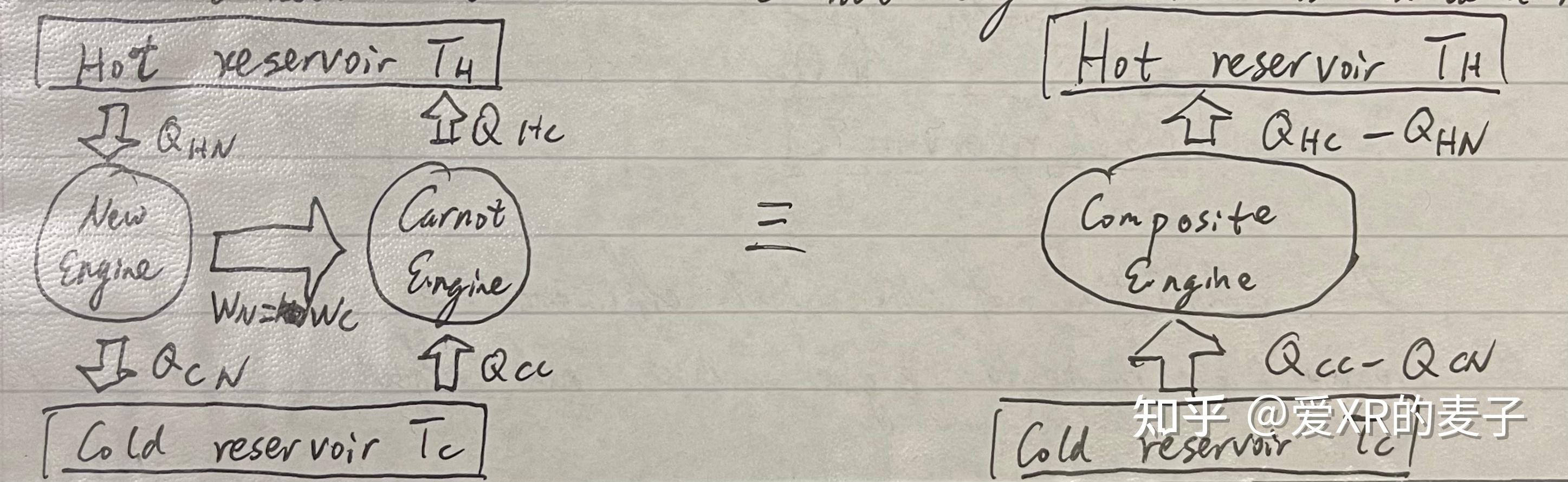
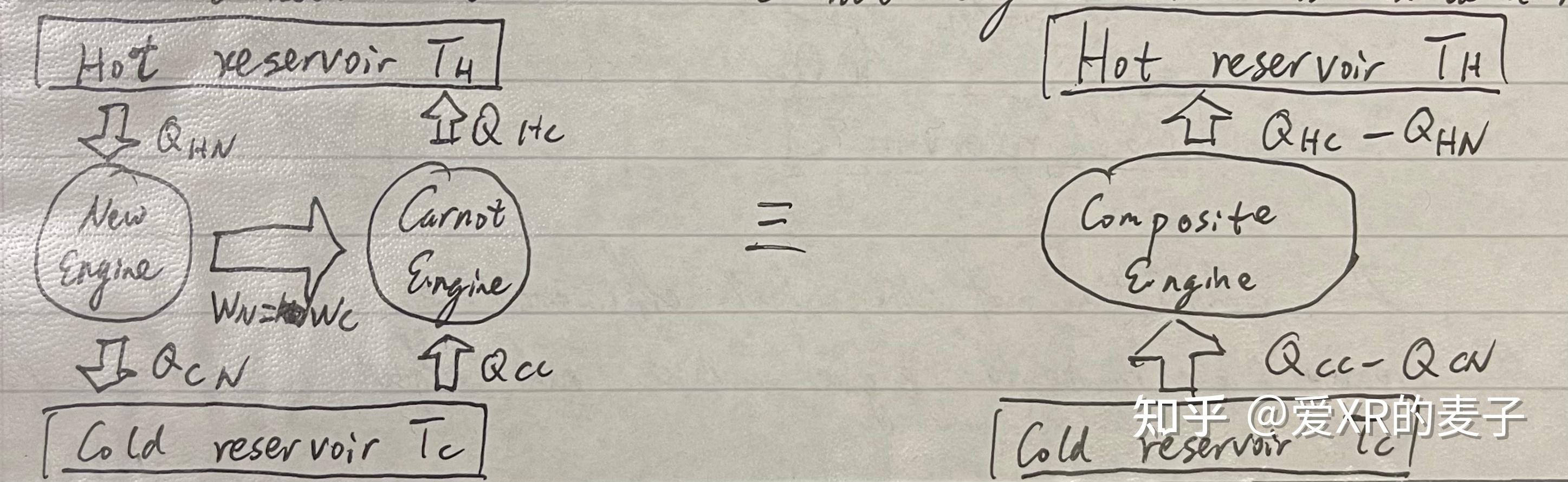
先假设有一个不可逆的引擎,但是有高于卡诺引擎的效率。将这个引擎与卡诺引擎相连。这个新引擎从温度高的热库吸收热量, ,传递到温度低的热库,
,并做功
;卡诺引擎则从温度低的热库吸收热量,
,传递到温度高的热库,
,也就是一个卡诺制冷机,并由新引擎对它做功,
。
因为我们让新引擎对卡诺引擎做功, ,因此我们也可以把它们两考虑成一个系统,这个新系统不对外做功。我们假设合成的系统,从温度低的热库吸收热量
,传递热量到温度高的热库
。
我们的假设是新引擎效率更高,所以
但是 ,
根据热力学第一定律
可以看出我们的合成系统确实如我们假设的一般,从温度低的热库吸收热量传递热量到温度高的热库。但它不做功啊!这就违背了热力学第二定律。所以一开始的假设无效:不可能存在一个有高于卡诺引擎效率的不可逆的引擎。违背卡诺定理也就是违背热力学定律。










如果认为本文对您有所帮助请赞助本站