摘要：在《狭义与广义相对论浅说》中，爱因斯坦对相对论进行了科普，提出了时间与空间的相对性。狭义相对性原理是，若K’是相对于K作匀速运动而无转动的坐标系，则自然现象相对于K’的实际演变与相对于K的实际演变依据同样的的普遍定律。狭义相对论中的（笛卡尔）坐标变换由洛伦兹变换决定，空时连续区是欧几里得连续区。广义相对性原理是，所有参考物体，无论运动状态如何，对于表述普遍自然界定律都等效。广义相对论中的（高斯）坐标可由任意变换决定，空时连续区是非欧几里得连续区。

一、 狭义相对论

1. 几何命题的物理意义

· 几何学命题由概念和公理出发，通过逻辑推理得出，所以命题的真实性归结于公理性的真实性，然而真实这一概念与几何学不符，因为几何学不涉及实在的经验客体。

· 如果在几何学中加入这一命题：在一个在实践上可视为刚体的物体上的两点永远对应同一距离（直线间隔），而与我们我们可能使该物体发生的位置变化无关，欧几里得几何学便可视为物理学的分支，而几何命题真实性问题的提出也有了合法性。

· 这种意义下几何命题的真实性由不完整的经验为基础，而在广义相对论中，欧几里得几何命题的真实性是有限的。

2. 坐标系

· 长度测量的基础是规定一个可作为量度标准的距离S，在A、B两点作直线连接，从A出发，重复记取距离S，直到B位置，记取的次数即AB的数值量度。

· 描述一事件发生的地点或一物体在空间中的位置，可以以能够在一刚体（参考物体）确定该事件或该物体的相重点为根据，此方法的前提是位置在刚体表面，且刚体表面存在可区分的点。

· 如果在描述位置时考虑数值量度而非刚性参考物体上的标定位置，会摆脱一些限制，笛卡尔坐标系可达到此目的；笛卡尔坐标系中有三个相互垂直的平面，由一刚体连接，事件发生地点由该地点向三个平面所做垂线的长度确定。

· 事件在空间中位置的每一种描述都要使用为描述这些事件而必须参照的一个刚体，距离在物理学中一般以一刚体上的两个标记来表示。

3. 经典力学中的空间和时间

· 力学的目的在于描述物体在空间中的位置随时间的变化。

· 物体在空间中运动的位置变化因参考物体的改变而改变，故空间中位置变化指的是相对于一个在实践上可看作刚性的参考物体的变化。

· 我们还需要描述对于运动轨迹的每一个点，物体在什么时刻位于该点，而这需要时间的概念，在经典力学中，我们可以使用时钟每一声滴答声记下的时间。

4. 伽利略坐标系

· 伽利略-牛顿力学的基本定律（惯性定律）是：一物体在离其它物体足够远时，一直保持静止状态或匀速直线运动状态。

· 如果要遵循惯性定律，需参照恒星在其中不做圆周运动的坐标系来考察物体的运动，即伽利略坐标系，伽利略-牛顿力学的定律只在伽利略坐标系中有效。

5. 狭义相对性原理

· 若一质量m相对于一坐标系K作匀速直线运动，另一坐标系K’相对于K作匀速平移运动，则m相对于K’作匀速直线运动。

· 若K为一伽利略坐标系，则其他每一个相对于K作匀速平移运动的坐标系为伽利略坐标系。

· 狭义相对性原理表述为：若K’是相对于K作匀速运动而无转动的坐标系，则自然现象相对于K’的实际演变与相对于K的实际演变依据同样的的普遍定律。

· 支持相对性原理正确性的第一个论据是，经典力学对天体实际运动的描述具有惊人的精确度，在力学领域相对性原理具有很高的准确度，如果它在物理另一个领域无效，从先验的角度看不太可能。

· 支持相对性原理正确性的第二个论据是，如果相对性原理不成立，则彼此作相对匀速运动的伽利略坐标系对描述自然现象不等效，故我们可以选定一个绝对静止的坐标系K0，而其他伽利略坐标系K都是运动的；这样自然界定律与物理系统行为与地球在任一时刻的运动方向有关，且地球公转速度方向的变化说明地球不可能全年相对于K0静止，但地球物理空间的各向异性没有被观察到。

6. 经典力学中的速度相加定理

· 若人走路前进的速度为w，而人所在的火车前进速度为v，那么人相对于路基的前进速度是v+w，这是经典力学的速度相加定理，而它实质上是不成立的。

7. 光的传播定律与相对性原理的表面抵触

· 光在真空中的直线传播速度为c=300000000米/秒，这一速度与光的颜色和放光物体的运动速度无关。

· 如果速度相加定理成立，那么沿路基发出的光线相对于同方向运动速度为v的火车运动速度为c-v<c，但这与相对性原理相抵触，因为光在真空中的传播速度无论以火车还是路基作为参考物体都应相同。

· 相对性原理自然而简单，而洛伦兹的电动力学和光学研究证明真空中光速恒定定律的真实性，这是就产生了狭义相对论，在此理论中相对性原理和光的传播定律并不抵触。

8. 物理学的时间观

· 对于理论物理学家，在他可能判断一个概念在实际情况中是否被满足之前，此概念还不能成立，所以对于同时性这一概念，我们需要用观测的方法来检验。

· 若要检测雷电是否同时击中铁轨上相距甚远的两地A和B，可以让一位观察者处在AB中点M，他有一观测装置（互成90度的两面镜子），使他用眼能一下在观测到A和B，若此观察者视神经同时感受到两个雷电闪光，那么它们就是同时的。

· 此检测方法要求光从A到M和从B到M的传播速度相同，这不是关于管的物理性质的假定或假说，而是为得出同时性的定义按自由意志作出的规定。

· 为得出物理学的时间定义，我们把构造完全相同的钟放在坐标系的诸点，并校准它们，使指针（按上述描述）同时指向相同的位置，这样时间可定义为放置在该事件最邻近处的钟的读数。

· 此定义中规定假定相同的钟以同样的时率走动，也就是说如果在一个钟指针指着某一特定位置的（按上述描述）同时，其他钟的指针也指着相同位置，那么这些钟的指针位置总是同时的。

9. 同时性的相对性

· 对于路基来说同时的两个时间，对于以恒速v运动沿某一方向行驶的火车来说并不是同时的。

· 若A、B两处雷击相对于火车同时，那么在A（左）、B（右）闪电所发出的光在AB中点M相遇，在火车上对应的A、B两处的中点M’，在雷电闪光发生时与M重合，但M’以速度v沿火车行驶方向（右）运动，故位于M’的观察者先看到B发出的光线，后看到A发出的光线。

· 每一参考物体都有它的特殊时间，关于一事件时间的陈述，若没指出相对于哪一参考物体，则无意义。

· 在相对论之前，物理学隐含地假定时间的陈述具有绝对意义，与参考物体的运动状态无关，此假定与同时性定义不相容，若抛弃此假定，真空中光的传播定律与相对性原则便不抵触。

· 时间的绝对性说若在火车上的人每秒相对于车厢走距离w，那么他每秒相对于路基也走距离w，然而时间具有相对性，故在火车上走动的人相对于路基走距离w的人，从路基上的时间看不一定需花一秒钟。

10. 距离概念的相对性

· 在速度为v的火车上，观测者用量杆从一点一下一下地量到另一点，量的次数便是火车上两点的距离。

· 如果在火车上的两点A’和B’在路基上对应这样的两点A和B，使其在一特定时刻t各为A’和B’所通过，那么从先验角度讲，用量杆沿路基量取的A、B两点距离不一定与火车上量取的A’、B’两点距离相同。

11. 洛伦兹变换

· 我们想要寻找各事件相对于一参考物体的地点和时间与各该事件相对于另一参考物体的地点和时间的这样一种关系，使得光无论相对于哪个参考物体穿比速度都是c。

· 一事件相对于坐标系K在空间中由坐标平面的三条垂涎x，y，z表示，时间由t表示，相对于另一坐标系相应地用x’，y’，z’，t’来表示。

· 若已知一事件相对于K的四个量值，我们想要得到该事件相对于K’的四个量值，使得同一条光线相对于K和K’都满足真空中的传播定律，则需要洛伦兹变换：

· 若按照经典力学中时间和长度具有绝对性的假设，我们得到的是伽利略变换：

在洛伦兹变化中以无穷大代替光速c，便得到伽利略变换。

· 若真空中光的传播定律在坐标系K中被满足，x=ct，那么通过洛伦兹变换得到

那么x’=ct’，即若真空中光的传播定律在坐标系K’中也被满足。

12. 量杆和种在运动时的行为

· 沿K’的x’轴放一刚性米尺，始端与x’=0重合，终端与x’=1重合，米尺相对于K的长度根据洛伦兹变是

而米尺相对于K以速度v运动，故刚尺在运动时比静止时长度更短，且运动越快长度越短，当速度v=c时，长度为0，当速度更大长度为虚值，故光速c是任何实在物质不能达到或超越的极限速度。

· 相对于K静止的在x轴上的米尺相对于K’的长度也是

故相对性原理得到满足。

· 一个永久放在K’原点的钟在t’=0和t’=1时报时两次，相对于K经过的时间是

故钟在运动时比静止时走的更慢，当速度v=c时，时间走得无限慢。

13. 速度相加定理和斐索实验

· 假设一个质点相对于坐标系K’按方程x’=wt’运动，那么它根据伽利略变换相对于坐标系K的运动速度是v+w，而根据洛伦兹变换相对于坐标系K的运动速度是

· 斐索实验想要检测的问题是，加入光在某种静止的液体中以速度w传播，那么光在管内以速度v流动的该液体中的传播速度是多少？根据相对性原理，由于光相对于液体的传播速度总是w，液体相对于管的运动速度是v，我们想求光相对于管的运动速度。

· 实验结果与按洛伦兹变换和相对论推出的速度相符，此外，塞曼的实验结果表明测的的速度的误差恒保持在百分之一以内。

· 洛伦兹在相对论提出之前就提出了关于此现象的理论，原始理论由麦克斯韦-洛伦兹电动力学建立，故相对论由电动力学发展出来，是相互独立组成电动力学的各假说的综合。

14. 相对论的启发作用

· 每一个普遍的自然定律必须是这样建立的：若我们用坐标系K’的空时变量x’，y’，z’，t’代替坐标系K的空时变量x，y，z，t，则经过变换后该定律的形式完全相同，也就是说，普遍的自然定律对于洛伦兹变换是协变的。

15. 狭义相对论的普遍性结果

· 狭义相对论对电动力学和光学的理论预测并未作多少修改，但简化了理论的结构和定律的推导，并减少了构成理论基础的独立假设的数目。

· 经典力学需要修改才能与像一相对论一致，此种修改只对速度比光速小的不多的高速运动定律，即电子和离子的运动定律有影响，在其他运动中经典力学和狭义相对论所得结果相差极微。

· 具有质量m的质点的动能不再由公式

表达，而是由公式

表达，故无论产生加速度的能量多大，速度v必然小于光速c。

· 在相对论创立之前，能量守恒定律与质量守恒定律是相互独立的，而根据相对论，这两个定律已结合成一个定律。

· 若一物体以速度v运动，以吸收辐射的形式吸收了能量E0，若速度不变，则该物体吸收能量后的能量是

这样可得出，若一物体吸收能量E0，其惯性质量增加

故物体的惯性质量不是恒量，而是随能量的变动而变动。

· 目前此关系式还无法用实验验证，我们还不能使一个物系发生的能量变化大到引起惯性质量变化的程度，所以经典力学才将质量守恒确立为一个独立的定律。

· 用阿尔法粒子、质子、氘核、中子或伽马射线轰击元素引起的核变已经充分证实了质能相当性关系式

· 由于电磁超距作用的法拉第-麦克斯韦解释获得成功，物理学家确信，像牛顿引力定律那样不涉及中介媒介的瞬时超距作用不存在，按照相对论，瞬时超距作用应被按光速传播的超距作用代替。

16. 经验和狭义相对论

· 相对论可以解释地球对恒星的相对运动对于恒星传到地球的光的效应，这些效应与经验相符；效应一是地球绕日运动引起恒星视位置的周年运动（光行差），效应二是恒星传到地球的光的光谱线位置与地球上光源所产生的相同光谱线位置相比有微小的移动（多普勒效应）。

· 支持麦克斯韦-洛伦兹理论的论据大多支持相对论，但有两类实验事实，若不引用相对论，便无法用麦克斯韦-洛伦兹理论来表示。

· 阴极射线和贝塔射线由惯性很小速度很大的带负电的粒子（电子）组成，在对电子进行理论描述时，电动力学理论不能解释电子本性；构成电子的负的电质量在本身相互排斥的影响下必然离散，如果假定电质量的相对距离在电子运动过程中不变（经典力学刚性连接），则得到与经验不服的电子运动定律。

· 洛伦兹假定电子外形会在运动方向发生收缩，此假设没有被电动力学的事实证明，然而相对论推出了同样的运动定律，而无需借助关于电子结构和行为的假设，斐索实验也得出了相似的结论。

· 第二类事实设计地球在空间中的运动能否用地球上的实验来观察的问题，这类企图都得到了否定的答案，令人们很难接受。

· 若麦克斯韦-洛伦兹方程对坐标系K成立，而伽利略变换不容置疑，则这些方程对相对于K作匀速运动的坐标系K’不成立，那么必有一伽利略坐标系对一种特别运动状态具有物理唯一性；相对论之前的解释是K相对于空间中的以太静止，而所有相对于K运动的K’相对于以太运动。

· 物理学家试图探测以太漂移是否存在于地球表面，迈克耳孙的设想是在一个刚体上放置两面反光面相互面对的镜子，若系统相对于以太静止，那光线从一面镜子射到另一面再返回就需要确定的时间T，而若相对于以太运动，则需要不同的时间T’，且若相对于以太运动速度不变，垂直于镜面运动的T’与平行于镜面运动的T’是不同的，然而实验结果完全否定了这些假设。

· 洛伦兹和斐兹杰惹假定物体相对于以太的运动引起物体收缩，按相对论看，这种解释可行，但是并没有理由假定唯一坐标系的存在并引进以太和以太漂移的观念，运动物体的收缩由相对论两个基本原理推出，二造成收缩的首要因素不是运动本身，而是相对于参考物体的运动。

17. 闵可夫斯基四维空间

· 闵可夫斯基简称为世界的物理现象世界，是一个四维空时连续区，因为事件由x，y，z，t四个值描述，连续是指临近时间坐标可相差无穷小量。

· 相对论之前，时间充当着不同于空间坐标的独立角色，所以人们习惯于把时间看作独立的连续区，而不把世界看作四维连续区。

· 洛伦兹变换的第四方程表明时间失去了独立性，且当两事件相对于K时间差为零时，相对于K’时间差一般不等于零，两时间相对于K的空间距离成为该两事件相对于K’的时间距离。

· 闵可夫斯基发现相对论的四维时空连续区在最主要的形式性质方面，与欧几里得空间的三维连续区有明显的关系，为表示此关系，我们必须用

来代替通常的时间坐标t，这样时间坐标的作用就与三个空间坐标完全一样。

二、 广义相对论

1. 狭义和广义相对性原理

· 从狭义相对性原理来看，每一种运动都是相对运动，不管引用火车还是路基作为参考物体，普遍自然界定律的形式是完全一样的，也就是说，在参考物体中没有一个比另一是唯一的，与前一种表述不同，后一种表述不是由于推论自然成立，而只能被经验验证。

· 对于狭义相对性原理，我们的思路如下：假定存在以参考物体K，其运动状态使伽利略定律对它而言成立，一质点若不受外力作用并离其他质点足够远，则该质点作匀速直线运动；此外，所有相对于K作匀速直线无转动运动的参考物体（伽利略参考物体），对于描述自然界定律与K完全等效。

· 广义相对性原理的陈述如下：所有参考物体，无论运动状态如何，对于表述普遍自然界定律都等效。

· 若火车作匀速运动，车厢里的人不会感受到运动，而若火车作非匀速运动，此运动就会由物体相对于人的力学行为表现出来，故伽利略定律对于作非匀速运动的火车不成立，而若否定广义相对性原理并赋予非匀速运动特殊的物理实在性，却是不能成立的。

2. 引力场

· 从电磁现象可得出，没有中间媒介的超距作用是不可能的，如磁铁吸铁，磁铁在周围空间产生具有物理实在性的磁场，作用于铁块，我们应该用相似的方式看待引力。

· 地球对于掉落的石块的作用不是直接的，而是通过地球在周围产生的引力场，作用于石块并引起石块下落，当物体离地球更远，地球对物体的作用强度按确定定律减小；物体在其最邻近处产生一个场，场再离开物体各点的强度和方向由支配引力场的空间性质定律确定。

· 在引力场唯一影响下运动的物体得到一个加速度，此加速度与物体材料和运动状态无关，换句话说，按照牛顿定律，（力）=（惯性质量）x（加速度），而若引力引起加速度，（力）=（引力质量）x（引力场强度），所以

· 在同一引力场，加速度一样，故物体的引力质量与惯性质量之比一样，若选取适当单位使比值为1，则可得出物体的引力质量等于其惯性质量，此定律的解释是，物体同一性质按不同处境表现为惯性或重性。

3. 惯性质量和引力质量相等是广义相对性公理的论据

· 假设在一无所有的空间中有很大的一部分，离可感知质量遥远，基本满足伽利略基本定律所要求的条件，把一个大箱子作为参考物体，里面安置一个观察者，用绳子把自己拴在地板上；箱子外安装了系有缆索的钩子，缆索被以恒力拉动，箱子作匀加速运动上升，被我们在一个未用绳牵的参考物体中观察。

· 箱子的加速度要通过地板的反作用力才能传给箱子内的观察者，他必须用腿承受此压力，故他与站在地球上房间里完全一样，若他松手放开一物体，物体会作加速相对运动掉到地板上，观察者会判定，无论物体是什么，物体朝箱子地板的加速度总有相同量值。

· 观察者认为自己及箱子一个对于时间恒定的引力场中，他疑惑箱子在引力场中不降落，而当他发现系着缆索的钩子，便会认为箱子静止地悬挂在引力场中；我们不应认定他错了，虽然我们认定箱子相对于伽利略空间作加速运动，但也能认定箱子静止，故相对性原理可推广到相互作加速运动的参考物体。

· 这种解释的基础是引力场是一切物体获得相同加速度，也就是说，惯性质量和引力质量相等；假设箱子里的人将绳子一端系在箱子盖内面，另一端系在一物体上，绳子伸张，箱子里的人认为物体受到引力场中的引力，绳子张力由物体引力质量决定，箱子外的人认为绳子参与箱子加速运动传给物体，绳子张力由物体惯性质量决定。

· 人们可能会认为引力场的存在是一种表现的存在，或无论存在何种引力场，总能选取一参考物体使得对它而言没有引力场存在，这不是对于所有引力场都正确，只对特殊的引力场才是正确的。

· 若火车作非匀速运动，此运动就会由物体相对于人的力学行为表现出来，这种表现不仅可以归因于实在的加速度，也可以归因于对于时间而言可变的引力场。

4. 经典力学的基础和狭义相对论的基础在哪些方面不令人满意

· 经典力学的基本定律，离其他质点足够远的质点保持静止或匀速直线运动，只对具有某些特殊运动状态并相对作匀速平移运动的参考物体K有效，而相对于其他参考物体K’失效。

· 在经典力学或狭义相对论中，没有实在的东西能说明为什么物体对于参考物体K和K’的表现不同，此缺陷在参考物体运动无需外力维持，如匀速转动时，尤为突出，广义相对论能消除此缺陷，因为它对一切参考物体都成立。

5. 广义相对性原理的推论

· 广义相对性原理使我们以纯理论推出引力场性质，若已知一自然过程相对于一个伽利略参考物体K如何发生，便可以通过纯理论计算判定此自然过程对于相当于K作加速运动的参考物体K’如何表现。

· 相对于伽利略参考物体K，一道光线沿直线以速度c传播，而相对于作加速运动的参考物体K’，这道光线的传播路线不再是直线，故可得出，光在引力场中一般沿曲线传播；光当线穿过人们可利用的引力场，只有极微小的曲率，而当光线以掠入射方式经过太阳，曲率会很显著。

· 按照广义相对论，作为狭义相对论的基本原理之一的真空中光速恒定定律不是无限有效的，光线的弯曲只有在光的传播速度随位置而改变时才能发生；狭义相对论的有效性不是无限的，而只有不考虑引力场对现象影响时才是有效的。

· 狭义相对论和广义相对论的关系如同静电学和电动力学的关系一样，前者作为后者的极限情况存在。

· 相对于一个无论作何运动的参考物体K’来考察没有引力场的伽利略区域，相对于K’存在一个对于空间和时间可变的引力场，按照广义相对论，普遍引力场定律能够从这样的特殊引力场中推导出来。

6. 在转动参考物体上钟和量杆的行为

· 假设一空时区域相对于参考物体K不存在引力场，K对于此区域是伽利略参考物体，且狭义相对论的结果对于K成立；假设参考物体K’对于K作匀速转动，K’具有平面圆盘的形式，在其本身平面内围绕其中心作匀速转动。

· 在圆盘K’上离开盘心而坐的人感受到沿径向向外的一个力，相对于K静止的观察者会把这个力解释为惯性效应（离心力），而坐在圆盘上的观察者会根据广义相对性原理把圆盘看作静止的，因为他把作用于他身上的力看作是引力场效应。

· 圆盘K’上的观察者构造两个完全相同的钟，一个放在圆心，一个放在边缘，两个钟相对于K’静止；从伽利略参考物体K来看，圆心的钟无速度，而边缘的钟相对于K运动，所以第二个钟走的更慢，坐在圆盘中心旁的观察者也会观察到此现象，故无法根据相对于参考物体静止的钟得出时间和同时性的定义。

· 若圆盘K’上的观察者把标准量杆放在圆盘边上并使之与圆盘相切，从伽利略坐标系K看此杆长度小于1，然而如果把量杆沿半径方向放在圆盘上，从K看此杆不会缩短，这样观察者算出的圆周率比3.14…大，故欧几里得几何命题不能在引力场中严格成立，无法借助狭义相对论使用的方法规定下圆盘坐标。

7. 高斯坐标

· 按高斯的论述，可在桌面上画一个无限稠密的曲线系，并用一个实数表示一个u曲线，这些u曲线彼此不相交，桌面上每一点必有一条且仅有一条曲线通过，故每一点都有一个完全确定的u值；可以用同样的方式画出另一些v曲线，每一点的u值和v值就是该点的高斯坐标。

· 桌面上相邻两点P和P’对应的坐标是

其中du和dv表示极小值，同理，极小值ds可以表示P和P’的像是用一根小杆测量得到的距离

其中g11，g12，g22由u和v决定，这些量决定小杆相对于桌面的行为。

· 当桌面上的点相对于量杆构成欧几里得连续区，u曲线和v曲线便是欧几里得几何学相互垂直的中的直线，且

高斯坐标便成为笛卡尔坐标；高斯坐标只是两组数和面上点的缔合，此方法也可应用于高维连续区。

· 表述ds的方法只有在连续区内足够小的区域可被当作欧几里得连续区时才有效，如大理石桌面和局部温度变化，故正方形作图法的缺陷扩展到相当大一部分桌面才会明显表现出来。

· 高斯发明了对一般连续区作含有距离定义的数学表述的方法，一个连续区内每点可由若干数（高斯坐标）表示，坐标数量等于连续区维度，高斯坐标系是笛卡尔坐标系的逻辑推广。

8. 狭义相对论的空时连续区可当作欧几里得连续区

· 按照狭义相对论，我们用伽利略坐标系描述四维空时连续区，每个事件用四个坐标x，y，z，t（有物理意义）来确定，从一个伽利略坐标系过渡到另一个相对于此坐标系作匀速运动的另一个伽利略坐标系，洛伦兹变换方程完全有效，这些方程表述光的传播定律对于一切伽利略参考系有效。

· 闵可夫斯基发现洛伦兹变换满足以下条件

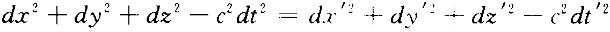
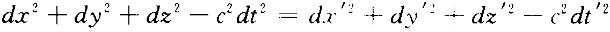
此条件确定了洛伦兹变换的有效性，而四维空时连续区相邻两点的

对于一切伽利略参考物体具有相同的值。

· 如果我们不选取实变量t而选取虚变量

作为时间变量，便可以按狭义相对论把空时连续区当作欧几里得四维连续区。

9. 广义相对论的空时连续区不是欧几里得连续区

· 按照广义相对论，当引力场存在时，光速必须依赖于坐标，而狭义相对论使用的坐标和时间由于引力场的存在而失效，故空时连续区不能被看作欧几里得连续区。

· 四维空时连续区可以用任意高斯坐标系作参照，一个事件用四个坐标x1，x2，x3，x4（无物理意义）来确定；一个永久存在的点需要无穷多组的坐标数值来描述，这些紧密的点形成一根线，连续区中任意的线对应运动的点，而只有关于这些点会合的陈述才具有物理意义，而用数学表述，会合意味着两根代表运动的点的线有一组特别坐标值彼此共同。

· 当我们描述一个相对于参考物体运动的点，我们陈述的是这个点与参考物体各特定点的会合，我们也可以借助物体和钟的会合和钟指针和标度盘上各点的会合确定时间值，用量杆进行空间测量也是同理。

· 每一个物理描述可分为多个陈述，每一陈述涉及A、B两事件的空时重合，并由两事件的四个高斯坐标表达，此描述代替借助于参考物体的描述，不会受到欧几里得特性的限制。

10. 广义相对性原理的严格表述

· 广义相对性原理的严格表述是，所有高斯坐标系对于表述普遍自然界定律在本质上是等效的，也就是说，对高斯坐标应用任意变换，这些方程变换后形式相同，因为任一变换（不仅是洛伦兹变换）都是从一个高斯坐标系到另一个高斯坐标系的过渡。

· 狭义相对论和没有引力存在的伽利略区域相关，伽利略参考物体是一个刚体，其运动状态要求使孤立质点作匀速直线运动的伽利略定律对此刚体成立。

· 把伽利略区域引入非伽利略参考物体，对于这些物体便存在特殊引力场，引力场中没有具有欧几里得性质的刚体，虚设的刚性参考物体对于广义相对论无用，钟的运动由于受到引力场影响，借助于中作出的时间的物理定义无法达到狭义相对论中同样程度的真实感。

· 我们使用非刚性参考物体，此物体不仅运动是任意的，而且在运动中可以发生形变，钟无论遵循什么不规则运动，都可以用来确定时间，每个钟固定在非刚体参考物体的一点，空间中相邻的钟彼此相差无穷小量，我们把非刚性参考物体上每一点当作一个空间点，相对于空间点静止的质点就当作静止的，广义相对性原理要求这些非刚性参考物体都可以用来表述普遍自然界定律。

11. 在广义相对性原理的基础上解引力问题

· 若参照参考物体K’的任一高斯坐标系来考察此区域，相对于K’存在一引力场G，我们把量杆、钟和质点相对于K’的行为解释为在G影响下的行为 ，并假设这些影响将按相同定律发生下去。

· 通过坐标变换由伽利略特殊情况导出的引力场定律不是普遍的，为得到普遍引力场定律，我们应推广这些定律，使其满足广义相对性原理，且当任何物质堆砌激发一个场的效应，只有惯性质量/能量是重要的，且引力场加上物质必须满足能量和冲量守恒定律。

· 这样由广义相对性公理导出的引力论，可以消除经典力学的缺陷，解释惯性质量和引力质量相等的经验定律，也能解释一个经典力学无法解释的天文观测结果。

· 如果引力场相当弱，且引力场内所有相对于坐标系运动的质量的速度比光速小得多，我们就可以近似得到牛顿引力理论，而无需质点间吸引力与质点距离平方成反比的假定。

· 按照牛顿理论，行星沿椭圆轨道绕恒星运行，此椭圆轨道相对于恒星系固定不变，此陈述的唯一观测例外是离太阳最近的水星，它的轨道缓慢地在轨道平面内沿轨道运动方向转动；按照广义相对论，每一个绕日运行的行星椭圆轨道都会按此方式转动，只是其他行星的转动太小无法观测到。

· 另外两个只能从广义相对论推出的推论，光线因太阳引力场发生弯曲，以及来自巨大星球的光的谱线相比于地球上由同一种原子产生的光谱线有位移，均得到观测证实。

三、 对于宇宙的考虑

1. 牛顿理论在宇宙论方面的困难

· 就空间和时间而言，宇宙是无限的，虽细微部分物质密度变化很大，可平均来说，无论多远，恒星群种类和密度均类似，而牛顿理论要求宇宙具有某种中心，中心星群密度最大，而向外走星群密度逐渐减小，非常遥远处成为一个无限的空虚区域。

· 这种理论导致的结果是，从恒星中发出的光和恒星系中个别恒星不断奔向无限空间，一去不返，且不再与自然客体发生相互作用，有限的物质宇宙注定将逐渐而系统地被削弱。

· 希来哲对牛顿定律提出修正，假定对于很大的距离，两质量间吸引力比按照平方反比定律减小得更快，这样物质密度便可能处处一样，而不会产生无限大的引力场，但这种修改和复杂化没有理论依据，与牛顿理论相比，并没有建立在更普遍的原则上。

2. 有限而又无界的宇宙的可能性

· 非欧几里得几何学的发展导致，我们虽可以怀疑宇宙空间的无限性，却不会与思维规律或经验冲突。

· 设想在二维空间中存在持有扁平工具（刚性量杆）的扁平生物，它们的宇宙是二维的，延伸到无限远处，他们的宇宙可以容纳无限多用杆子构成的相同的正方形，所有杆子代表同样的距离，与位置无关。

· 另一种二维生物生活在球面而非平面上，这种生物与它们的量杆与球面完全贴合，它们不能认为它们的几何学是平面几何学，因为它们想实现的直线实则是曲线，从三维生物看这些直线是大圆，有确定的有限长度，可用量杆测出，这些生物的宇宙是有限而无界的。

· 这些生物从一点出发，沿所有方向画出等长直线，把连接这些线自由端的线称作圆，按欧几里得几何学，圆周与半径之比是pi，与圆的直径大小无关，而球面上圆周与半径之比是

此值小于pi，且圆半径r与世界球半径R之比越大，此值与pi差别越大，而若球面上的部分非常小，球面生物便会认为自己居住在欧几里得平面，以为球面上微笑的部分与平面上同样大小的部分相差甚微。

· 在所有闭合曲面中，只有球面满足曲面上所有点等效，世界球是一个等曲率曲面；二维球面宇宙的三维类比是黎曼的三维球面空间，它的点都等效，并具有由半径确定的有限体积，此三维球面空间同样也是有限而无界的。

· 我们从一点向所有方向拉出绳索，并用量杆在绳索上选取距离r，具有长度r的绳索的所有自由端点在一个球面上，如果在欧几里得平面，测出的曲面面积是

而在球面宇宙，测出的曲面面积小于此值，随着r增大，此面积从零增加到由世界半径确定的最大值，但若r继续增大，此面积降缩为零，从起始点辐射出的直线相距边缘，然后又相互趋近，直到相会于与起始点相对的的对立点。

· 另一种弯曲空间是椭圆空间，其中两个对立点是等样的，椭圆宇宙可被看作一个中心对称的弯曲宇宙。

3. 以广义相对论为依据的空间结构

· 根据广义相对论，空间的几何性质不是独立的，而是由物质决定的；对于一个适当的坐标系，诸星的速度比光的传播速度小的多，故若将物质看作静止，就能在粗略的近似程度上得出关于宇宙性质的结论。

· 我们的宇宙和欧几里得宇宙仅有微小的差别，即使太阳那样大的质量对于周围空间度规的影响也极其微小；就几何学而论，我们宇宙的性质类似于一个曲面，它在各个个别部分上不规则地弯曲，但整个曲面与平面无显著差别，这就是准欧几里得宇宙，其中物质平均密度必然等于零。

· 如果物质是均匀分布的，宇宙就必然是球形或椭圆的，由于实际上物质的细微分布不均，实在的宇宙在其各个个别部分上与球形有出入，即宇宙是准球形的，这个宇宙必然是有限的。

参考文献：

爱因斯坦，《狭义与广义相对论浅说》

转自本人豆瓣账号鹦鹉螺