投资专有技术变化引入投资专有技术变化的居民效用最大化居民的效用函数引入投资专有技术变化的居民效用最大化式中,假设,由资本积累方程...

投资专有技术变化
引入投资专有技术变化的居民效用最大化
居民的效用函数
引入投资专有技术变化的居民效用最大化
式中,假设,
由资本积累方程得到
式中,确定了一个单位产出可购买的资本数量,代表了当前生产性资本的技术状态,这样,投资可定义为
构建引投资专有技术变化的居民效用最大化问题的拉格朗日函数
一阶条件为
厂商利润最大化
厂商生产函数
式中,是全要素或部门中性的生产率,
。则厂商利润最大化问题为
一阶条件为
整理,得生产投入的价格
模型方程及参数校准
模型经济的竞争性均衡由刻画内生宏观经济变量和全要素生产率
以及专有技术
等方程来给出。模型方程为
模型参数集合
其中,:资本生产率的技术参数,典型值
;
:经济主体对未来效用相对于现在效用的评价,典型值
;
:资本存量的实际折旧率,典型值
;
:个体对消费-闲暇决策的偏好,典型值
;
:全要素生产率冲击过程中的自回归参数,典型值
;
:全要素生产率服从的随机过程中的误差项的标准差,典型值
;
:投资专有技术冲击过程中的自回归阐述,典型值
;
:投资专有技术服从的随机过程中的误差项的标准差,典型值
;
数值计算
import metakernel; metakernel.register_ipython_magics()%kernel matlab_kernel.kernel MatlabKernel%%writefile model6.modvar Y, C, I, K, L, W, R, A, Z;varexo e, u;parameters alpha, beta, delta, gamma, rho1, rho2;alpha = 0.35;beta = 0.97;delta = 0.06;gamma = 0.40;rho1 = 0.95;rho2 = 0.95;model;C = (gamma / (1 - gamma)) * (1 - L) * (1 - alpha) * Y / L;1 = beta * (Z * C / (Z(+1) * C(+1))) * (Z * alpha * Y(+1) / K + (1 - delta));Y = A * (K(-1) ^ alpha) * (L ^ (1 - alpha));K = Z * I + (1 - delta) * K(-1);I = Y - C;W = (1 - alpha) * A * (K(-1) ^ alpha) * (L ^ (-alpha));R = alpha * A * (K(-1) ^ (alpha - 1)) * (L ^ (1-alpha));log(A) = rho1 * log(A(-1)) + e;log(Z) = rho2 * log(Z(-1)) + u;end;initval;Y = 1; C = 0.8; L = 0.3; K = 3.5;I = 0.2;W = (1 - alpha) * Y / L;R = alpha * Y / K;A = 1;Z = 1;e = 0;u = 0;end;steady;check;shocks;var e; stderr 0.01;var u; stderr 0.01;end;stoch_simul;Writing model6.mod%%kxdynare model6.mod
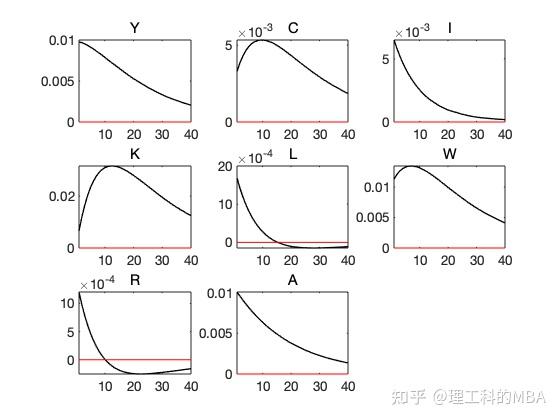



投资专有技术冲击
投资专有技术冲击对消费的影响是负的,这是因为新资本的生产率高于已安装的资本存量的生产率,从而投资于新资本更有利润,这导致投资增加并积累到资本存量中,投资专有技术冲击使得单位投资相对于单位消费更加便宜,这样就产生了消费与储蓄的跨期替代效应,以及消费与闲暇的期内替代效应。
















如果认为本文对您有所帮助请赞助本站