本文作者：蒋迅，[遇见君]这里特别感谢蒋老师一直来的关注和支持!

布赖恩·比尔斯顿（Brian Bilston）是一位奇特诗人。没有人知道他的来历，只知道他有一天突然在社交媒体上发了一个微博（他自己都不知道算不算是一首诗），更多地像是一组精心挑选的字词，仅仅是为了满足微博要求的 140 字限制。当然他发的微博看上去像是一首诗，而且竟然被一位有点名气的诗人点了一个赞。诗人随手的一点就开启了一个奇特诗人的新生。

斐波那契体诗

我也是在社交媒体上看到他的诗。抓住我眼球的是他的一首斐波那契体诗。后来我又看了他的其他作品。原来他的数学诗并不多，但确实与众不同，值得说上一句。

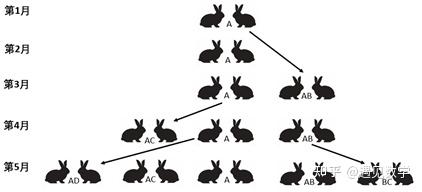
让我们就从斐波那契说起吧。为了让普通读者能够理解，我们先介绍一下斐波那契。数学上，斐波那契数列是意大利人斐波那契（Leonardo Fibonacci，1175－1250）研究的一个数列。他描述兔子生长的数目时做了如下的假定：

第一个月初有一对刚诞生的兔子，刚诞生的兔子在第二个月不会生育，从第三个月开始它们每月都可以生育，每月每对可生育的兔子会诞生下一对新兔子，兔子永不死去。

让我们记 ,。它们分别是第 月和第 月的兔子对的数量。因为刚出生的兔子在下一个月不会生新兔子，所以 。让我们引入 ，即在第 个月的时候兔子的数量是 。那么就有 。可以看到，在第 个月（），成立着 。于是我们得到一个数列：

比尔斯顿利用这个数列创作了一首诗。它的每一行的字数正好与这个数列相同。我们就称其为“斐波那契体诗”，或简称为“斐诗”。下面就是他的这首诗：

我们尝试把这首诗翻译如下：

对斐波那契数列有些了解的读者应该知道斐波那契可以用下面的斐波那契螺旋表示：

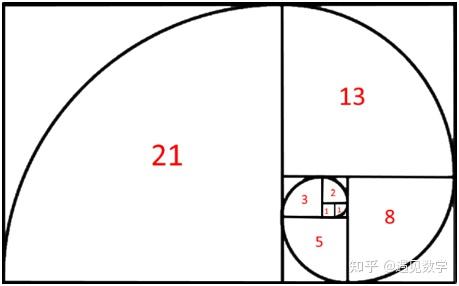
我们把这首诗和翻译也放到这个螺旋里。诗从螺旋的最中心开始逐步向外展开。

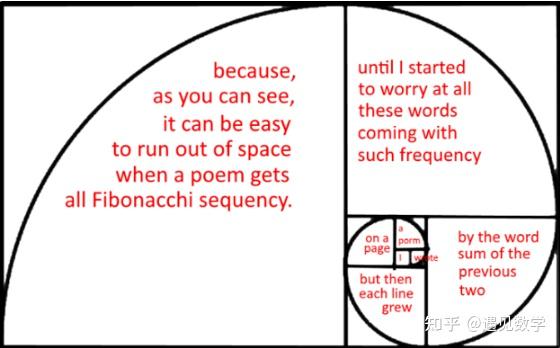
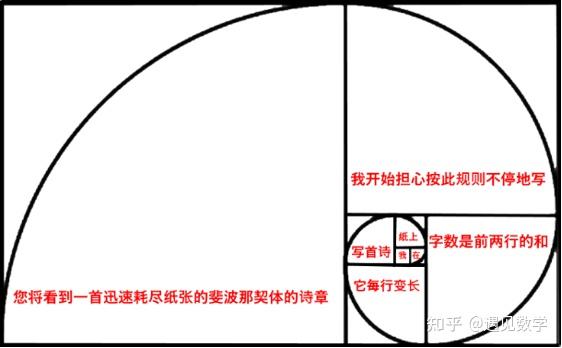
显而易见，在写这个诗体时，中文比英文有优越性：英文的每个字的长短不同，所以我们看到英文“word”这个词无法被放到单位方格里，而中文的“在”字则很容易安排进去。英文其他的句子也很难放到一行里，中文就轻易做到。 比尔斯顿的粉丝给了他热情的回应。比如下面网友 Jenny Boddington 的斐波那契体诗：

她把 Vi Hart 介绍斐波那契的三个视频巧妙地嵌入到这首诗里。油管上有 Vihart 的三个视频：“Doodling in Math: Spirals, Fibonacci, and Being a Plant [1,2,3]”。类似的视频有很多。还有网友 Renuka Dhinakaran 对比尔斯顿的夸赞：

当我把这个诗体介绍给好友张进后，他也颇有兴致地创作了一首《数》。

在张进的鼓励下，我也跃跃欲试一首《平面几何》：

所有的斐波那契体诗都有一个共同的特点就是没有结尾。正如比尔斯顿所说，你需要担心的是纸张不够空间。我的《平面几何》就在正要展开时戛然而止，颇有余言未尽的感觉。

斐波那契数列与黄金分割紧密联系，因为

正是黄金分割比例数。现在让我们做一点变化。我们仍然取头两项的值为 和 。即 。假定从第三项开始后的数列满足关系式：。于是我们得到数列：

这个数列与斐波那契数列有类似的性质。比如极限

叫做白银分割比例数。这个数列以英国数学家约翰·佩尔（John Pell，1611－1685）命名，叫做佩尔数列。如果以此作诗，那么就是佩尔体诗了。需要小心的是，佩尔体诗增长的更快。在这里试做佩尔体小诗一首：

维恩体诗

让我们再来看一首比尔斯顿的数学诗。诗体是个维恩图，我们就称为维恩体吧，也挺有意思。

维恩图也称文氏图或韦恩图等，是在集合论数学分支中用以表示集合的一种草图。最简单的是两个集合构成的维恩图。比如图 4 中黄色的圆圈（集合 A）可以表示所有的数学家的全体。蓝色的圆圈（集合 B）可以表示所有的哲学家的全体。黄色和蓝色的圆圈交叠的区域（叫做交集）包含所有的那些即使数学家又是哲学家的那些人。维恩图是 19 世纪英国的哲学家和数学家约翰·维恩（John Venn，1834－1923）在 1881 年发明的。因为他身兼数学家和哲学家两重身份，所以他在 A 和 B 的交集里。英国人伯特兰·罗素（Bertrand Russell，1872－1970）也在这个交集里。注意，现在我们有了三类集合：一类是数学家，一类是哲学家，还有一类是数学家又是哲学家。 比尔斯顿的维恩体诗“在十字路口上”（At The Intersection）如下：

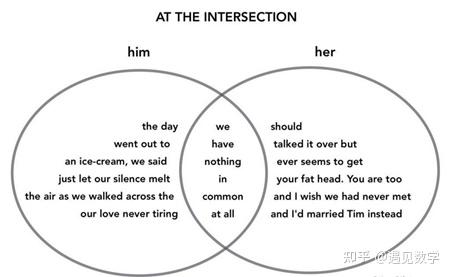
这个故事是讲的一对谈恋爱的情侣的心里对话。二人的思路完全不同，两人思路的交集部分就是说他们没有共同语言。我们尝试地翻译如下：

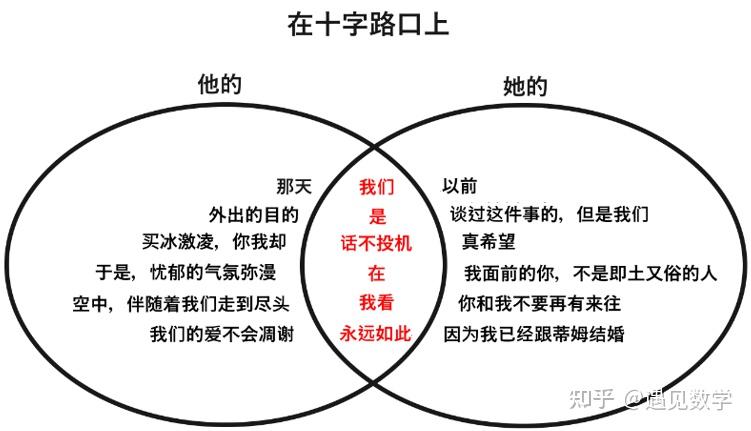
是不是很有意思？“他”和“她”各说各的话，他们没有共同语言。

网友们看了比尔斯顿的诗后也凑热闹创作了一些维恩体诗。

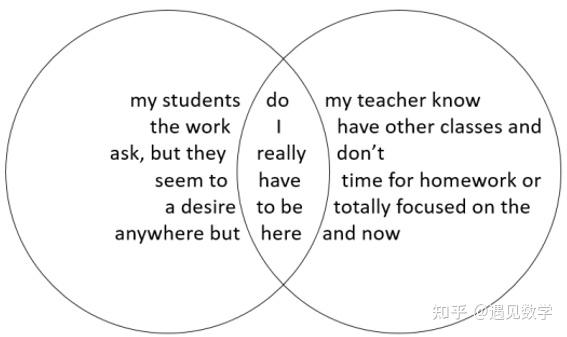
在我看来，这首“学生和老师“比比尔斯顿的“在十字路口上”更好。因为“在十字路口上”里的中间部分更像是“她的”话，而不像是“他的”话。而这首“学生和老师“的中间部分更像是双方的共同感受。这不正是维恩图中 A 和 B 的交集部分的含义吗？下面是另一首英文的维恩体诗《就业关系》：

如果创作维恩体诗的中文诗，可能最佳选择是传统的七言古体诗（即“七古”）藏字诗。我在下面试作一首七古藏字诗《春鸣秋声》：

这样一首诗可以看作是三首诗。第一首：

第二首：

第三首：

我没有试图把诗写成律诗，因为律诗对平仄押韵要求很严格，而且左边和右边需要分别成七绝，这对其中的藏尾诗部分要求太高。但从这个例子我们可以再一次看到中文诗词的威力，因为维恩体诗只是分为左右两首。

张进在给我热情指导的同时也做了一首七古藏字诗：

我们相信网友们有更为优秀的维恩体诗。

3.其他

比尔斯顿还有其他一些有趣的诗词。一首“表格”（cell）让人们想到了微软的表格软件 Excel。一首“助记”（Mnemonic）教人们如何记住一年中有哪些月份有 31 天。我们中国人有更好的办法：“一三五七八十腊，三十一天准不差”，再一次显示了中文的优越。“A Leaky Weekend”采用了竖版，这个在我们老祖先那里大量存在，不过对于西方人来说挺新鲜的。让我们用一首“炎热夏日写诗之烦恼”（The Problem of Writing Poetry on a Hot Day）来结束本文。读过之后，相信大家能想象到他的一首“大风天写诗之烦恼”（The Problem of Writing Poems on a Windy Day）该是一个什么样的风格了。

在西方，数学家们写诗是一个很常见的事情。张智民介绍过，一年一次的“有限元马戏团”活动里都会有数学家献诗的活动，笔者在马里兰大学读书的时候也记录过一位教授写的诗。那首诗记录在自己的博客里。现代中国也不乏诗人数学家：比如已故的苏步青和仍然活跃在诗坛的蔡天新。俄国数学家索菲娅·瓦西里耶夫娜·柯瓦列夫斯卡娅（Sofya Kovalevskaya，1850–1891）说过，“灵魂中不是诗人就不可能成为数学家。”在这里，我想抛砖引玉，请数学家们多多奉献你们的诗歌。

鸣谢：作者衷心感谢张进提供多处修改意见。

参考文献

Bryan Pitchford, Poetry at the Edge of the World, https://bryanjpitchford.com/2017/07/16/poet-brian-bilston/Brian Bilston, https://www.facebook.com/BrianBilston/ .A Fibonacci Poem, http://www.amathsteacherwrites.co.uk/a-fibonacci-poem/ .Sarah Glaz, Poetry Inspired by Mathematics, Proceedings of Bridges Pecs (2021), 35-43.张智民， 有限元马戏团，数学文化，第 10 卷第 4 期，2021.蒋迅，一首数学诗：新数学，http://blog.sciencenet.cn/blog-420554-724788.html .

遇见君: 欢迎各位老师和朋友评论区留下赋诗，把对数学之情融入其中，并且精彩的作品会有小礼物相赠。