上一篇中,我们假设了一个二体模型,找到了两个独立变量和,并将哈密顿量化简成下面的形式:接着,我们假设波函数可以作以下变化...

上一篇中,我们假设了一个二体模型,找到了两个独立变量 和
,并将哈密顿量化简成下面的形式:
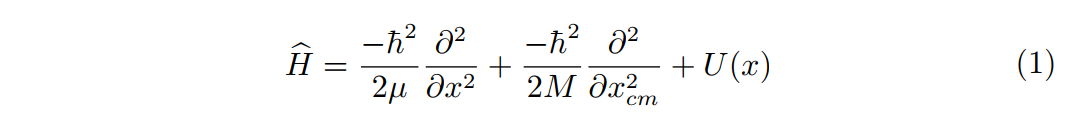
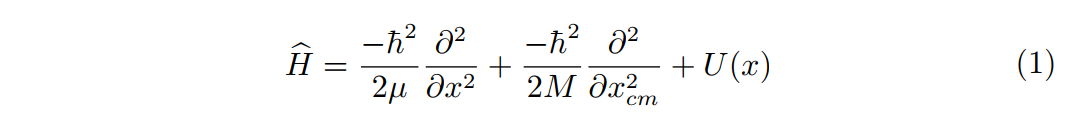
接着,我们假设波函数可以作以下变化:
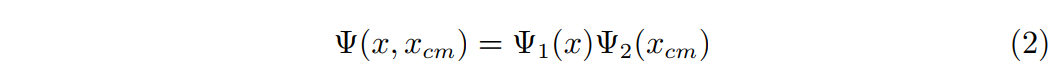
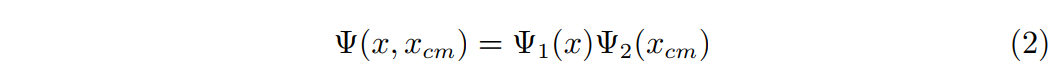
接着,对定态薛定谔方程一步步分离变量:


首先,将 (2) 式代入:
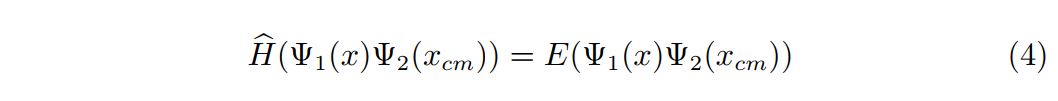
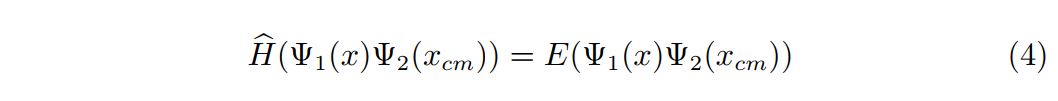
然后,我们先将 (4) 式左边展开化简:


于是,将 (4) 式左右两边同除 ,得:
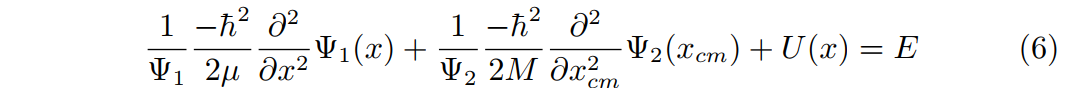
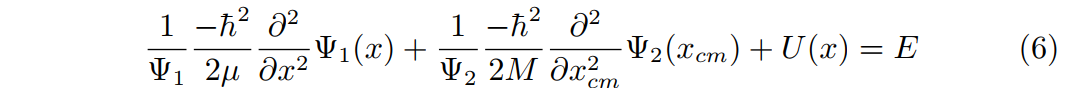
稍微整理一下,得到:


观察 (7) 式发现,左边第一次项只与变量 有关,第二项只与变量
有关,而等式右边却是一个常数
,于是只可能是左边的两项也分别等于一个常数,设为
和
, 于是有:
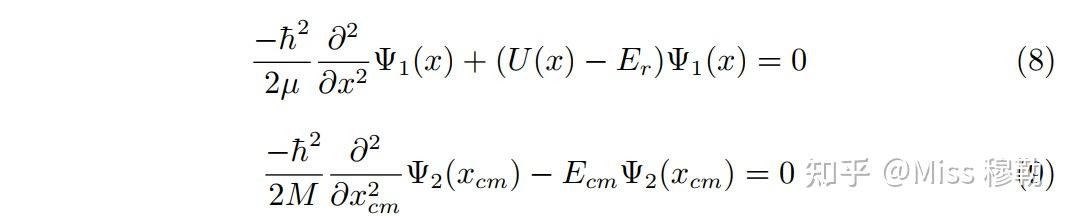
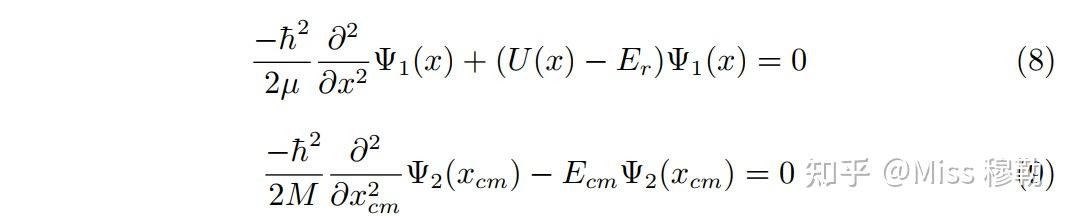
接着,在具体的情形下,通过各种限制条件,可以求解式 (8) 和 (9),分别得到 和
,也可以解得
和
的值,最后的总波函数就是两者波函数的乘积,总的本征能量
就是能量的加和。
从物理意义上而言,我们找到两个独立变量 和
,分别表征系统质心的运动和两个粒子的相对运动,因为它们的动量算符可对易,即
,所以通过分离变量的方法去化简定态薛定谔方程,从而找到本征波函数
,它是质心运动和相对运动的共同本征函数。
事实上,更一般的情况是,如果算符 和算符
对易,那么就一定存在一组共同完备的本征波函数,反之亦然。
在接下来的任务中,我们关注于求解氢原子的波函数,于是要从一维扩展到三维空间。但思路同样是将电子和原子核的运动转换成质心的运动和相对运动,并且重点求解相对运动的本征方程。
如果要求解氢原子能级,当我们关注电子和原子核的相对运动时,在三维空间有三个自由度,于是在上述推导基础上扩展,我们希望找到三个对易的本征算符,它们拥有着一套共同的本征函数集,也就是氢原子的本征波函数,最后也能够求得对应的本征值,也就是氢原子的分立能级。
以上内容
整理于
《张朝阳的物理课》5.20线上课










如果认为本文对您有所帮助请赞助本站