[二更] 上次很辛苦的更完了为啥意面不只断成两段的硬核物理解释，然后又发现有人做了个视频，用每秒1百万幅的高速相机捕捉意面断裂的瞬间。这个视频基本get到了文章理论部分的几个关键点。看公式头大的话就看下面的视频吧。

[更] 没想到真的有不少朋友对这种沙雕问题感兴趣，那我就更喽。先感谢那些点赞关注评论催更的朋友们！

评论区也有朋友指出有人发过这个关于意面的了，我也看了那个文章，应该是全文翻译的MIT的新闻稿。我本人是很喜欢那个文章的。但如果你不小心看过我这个专栏置顶的文章，你会发现我的侧重点是介绍这些看似沙雕的研究背后的硬核物理。看新闻稿肯定是轻松愉悦的，但那是别人咀嚼过的，真正有营养的东西的在原文献里面。

我们知其然，还要知其所以然。

这个文章可能要长文预警，介绍学术文献也不可避免地会出现公式和专业术语。当然，我深知斯蒂芬.霍金说过的真理：一个公式能吓跑一半读者！不过不要害怕，看不懂的地方略过也不会影响理解。【中括号内的都可以直接略过】。

以下：

本文打算介绍下2006年搞笑诺贝尔奖物理学奖。

为什么干意大利面折断的时候，总是多于两段？

获奖文章发表于 Physical Review Letters 95, 095505 (2005).

这个问题曾经让正牌诺贝尔物理学奖得主理查德.费曼非常的困扰。据说他花了几个小时在厨房里掰干意面，就为了搞清楚为什么意面总是断成好几段，而不只是两段？当然他的厨房实验失败了。更令他沮丧的是他也没有找到为啥意面总是断成好几段的合理解释。最终他也没能活着看到上面那篇文章的发表。

这个问题描述的是杆状物质的级联断裂现象。意面只是其中一个例子。

2021年奥运会撑杆跳的比赛现场就发生了类似的一幕：

2005年的PRL文章给出了理论解释。

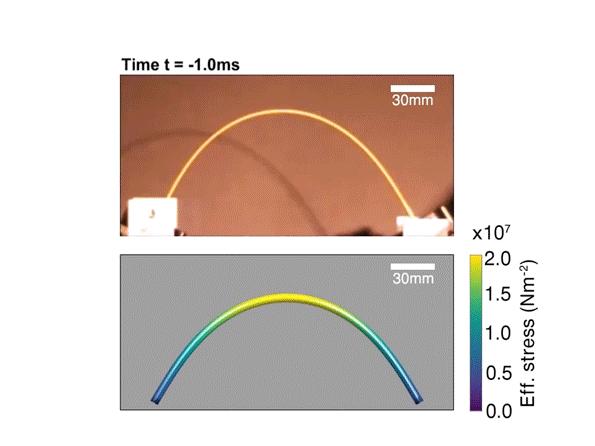
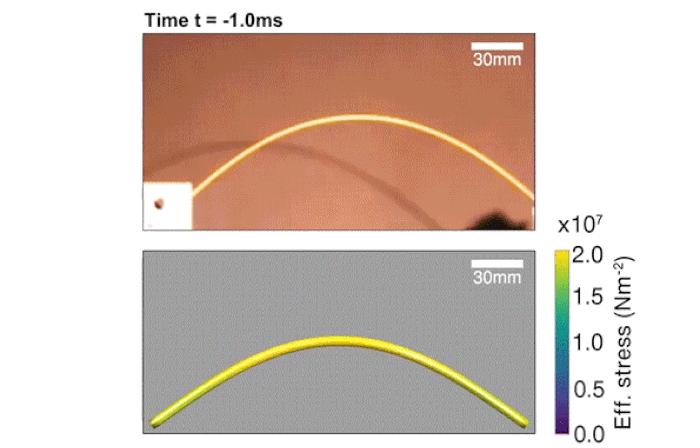
另外，2021年发表在美国科学院院刊PNAS上的一篇文章，来自MIT的科学家们则展示了如何控制意面的断裂，成功的将意面折成两段！

先卖个关子，这么沙雕的问题，有人关注的话再更吧！

有很多人催更，鞠躬、感谢！

以下内容大概会分成两部分：先介绍2006年搞笑诺奖的那篇PRL，理论解释为啥干意面总是断成好几段？若是大家还感兴趣的话，请留言，我再介绍2021年那篇PNAS，如何成功的将意面折成仅仅两段？

OK， 那篇PRL^{[1]来自法国巴黎第六大学的Basile Audoly和Sebastien Neukirch。}

先上结论：

波，弯曲震动波（flexural waves）。

当一根弯曲的意面被突然释放，意面两端的曲率在很短的时间内(微秒)迅速改变为零，激发震动波。震动波局域性的增加意面的曲率。当一个位置的曲率高于一定值后断裂发生。 断点位置的曲率迅速变化又激发新的震动波，导致更多的断裂出现，如雪崩过程。 结论似乎很简单，评论区很多朋友也都猜的八九不离十了。我们来看结论是怎么来的。

首先建立模型。我们考虑两端都被固定（或用手拿着）的意面，不断的用力使其慢慢弯曲以增大其曲率。当你把它掰断的那个瞬间我们记为初始状态 ，这个状态下意面的曲率 达到某一个阈值记为 。需要强调的是，在这个瞬间，第一个断裂发生，因此仅有两段意面，他们的一端仍然被固定（比如还在你手上），另一端因为断裂发生而被释放。瞬时状态可由下图1表示。

因为我们研究的是级联断裂过程，必然先会有初始的第一个断裂。但是我们不再讨论这个初始断裂是怎么发生的了，而将重点放在任意一半意面后续的动力学过程。阐述 的后续动力学过程如何导致新的断裂的发生。

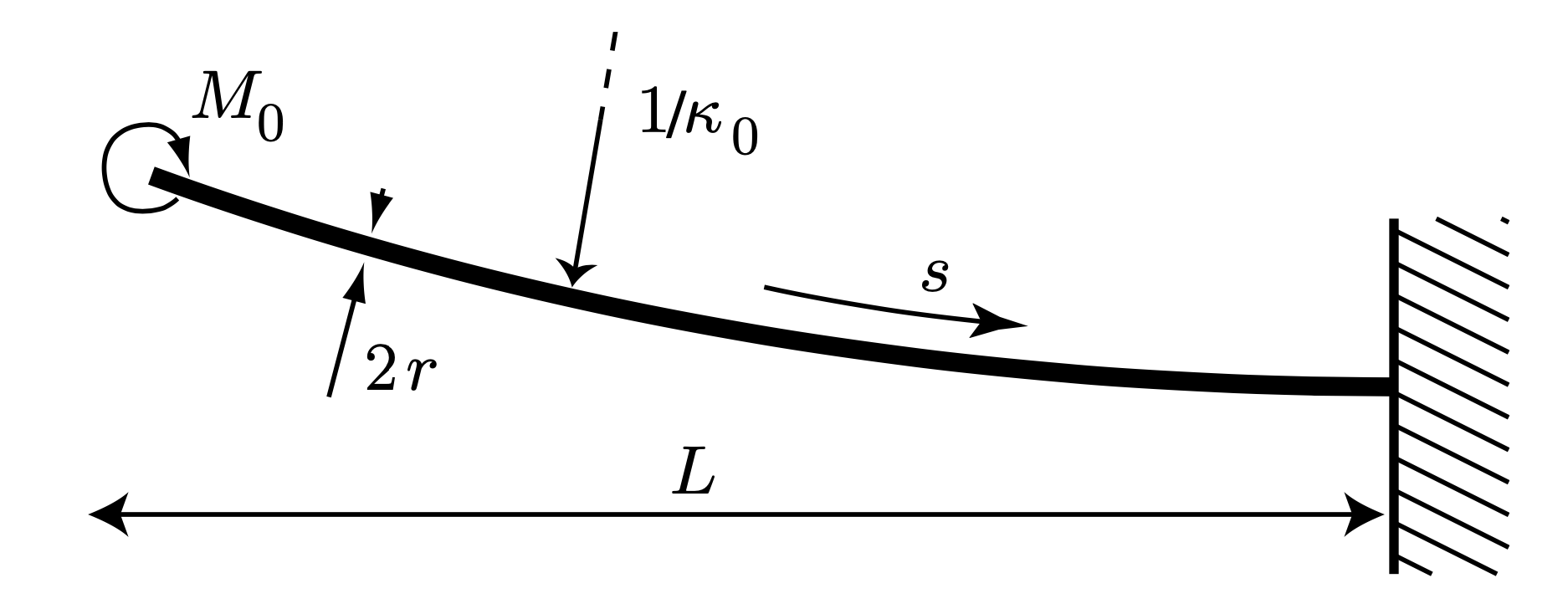
图1的模型模仿断裂发生的瞬时状态，意面一端固定在墙上，另一端被施加力矩 因而呈现出弯曲状态。显然，这一端的力矩被释放的过程等效于断裂发生的过程。因此这样一个模型能够模拟初始时掰断的两段意面其中一段。

在 时释放意面， 力矩 瞬间消失，原来的平衡态被打破。随后的动力学过程可由著名的基尔霍夫方程描述:【 ， 这里 为弧长坐标，逗号代表偏导。 表征意面柱状体的力学性质， ， 为杨氏模量， 为密度， 为横截面积， 为截面的转动惯量。这里的 正比于意面材料固有震荡周期 。】

对这个动力学方程有两点说明：1）线性假设，只考虑非常小的偏移。2）仅考虑图1平面内意面的变化过程。 有了动力学方程，求解 的话要先找初始条件和边界条件。【很显然两个边界，墙上固定的一端和自由端。固定端 处满足 , ；自由端 处满足 , 。 初始条件也有两个，最初在 处的曲率已知 ，以及初始时静止没有初速度，即初始曲率对时间的偏导为零 。】六个限制条件理论上能唯一的确定动力学方程的解 。

但是，不知道大家有没有注意到边界条件和初始条件存在不自洽的地方。因为自由端的边界条件要求 处的曲率为零(所以叫“自由”)，但是初始条件告诉我们了那一端的曲率在 时为 。这个不自恰的地方可以这样理解：意面的曲率正比于其内部力矩，在自由端力矩为零则曲率也应为零；这与我们最初认为的整个意面初始时各点的都具有相同的非零曲率不符。这是因为存在一个典型的边界层。厚度约为 的边界层对应一个特殊的时间尺度 ，其中 为横向断裂在意面内部传播的典型速度。这个1微秒的时间尺度相比于我们研究的级联断裂的时间尺度是很小的， 。

换句话说，自由端边界附近的初始曲率 在 的极短时间内恢复为零。这个弯曲状态突然被释放的过程造成一个突发的弯曲震动波。注意在时间尺度上 很短，而固有时间 很长，因此我们研究的过程的时间尺度满足 可称为中间渐近态。这样的情形下上面的动力学方程是可以获得解析解的。

具体的求解过程我还是略过吧，直接给出解的形式：

【 】

这个解里面的 为菲涅尔正弦积分。学过波动光学的一定知道近场菲涅尔衍射是什么样子的。

从这个解里面能得出重要结论：这个解描述的并非是速度恒定()的渐进波，而是自相似( )的解。 这种中间态的自相似通解不依赖材料的特性，不依赖初始的断裂过程，甚至不依赖固定一端的边界条件（实际上这个解的求解过程并没有用到 处的边界条件，关于自相似的概念请参考维基百科）。

下图2b直观的画出了这个解析通解随自相似参数 的变化规律。图2a则给出了数值解的图像。这个图像成功的捕获了上面讨论的几个重要的地方：首先，自由端 位置处的曲率 在几个数值计算步长内迅速减弱为零；其次，从自由端发出的震动波的速度随 变化；最后，在 震动波被边界反射回来之前，都具有自相似的形式。

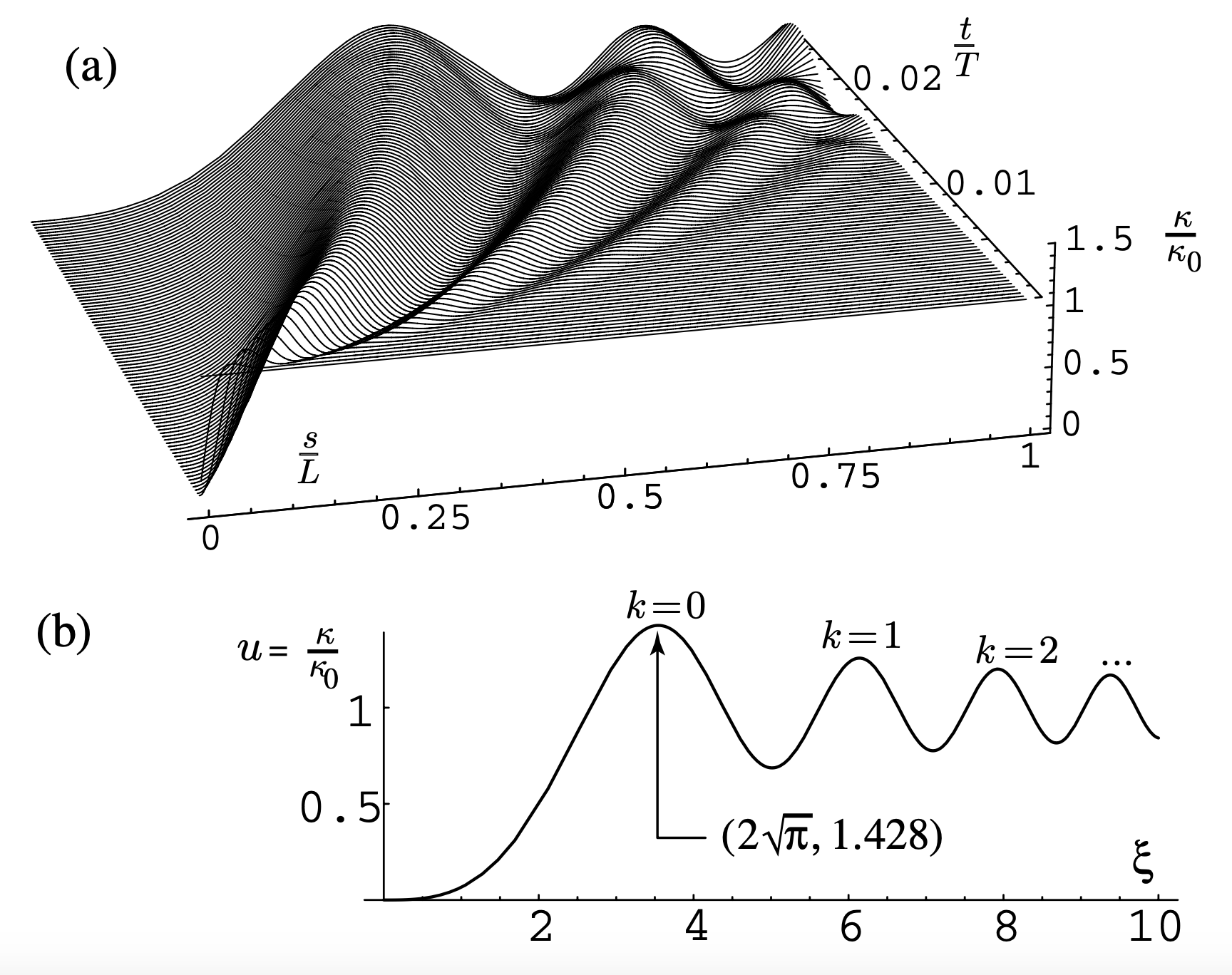
这个自相似解的一个关键性质为弯曲意面的局域曲率可以很大程度上超过最初的极限断裂曲率 。例如图2b在自相似参数为 处的曲率为1.428倍的初始曲率。这个系数是普适的，2倍于菲涅尔正弦积分的最大值。

这个理论预测的曲率增大得到了实验验证，如图3所示。

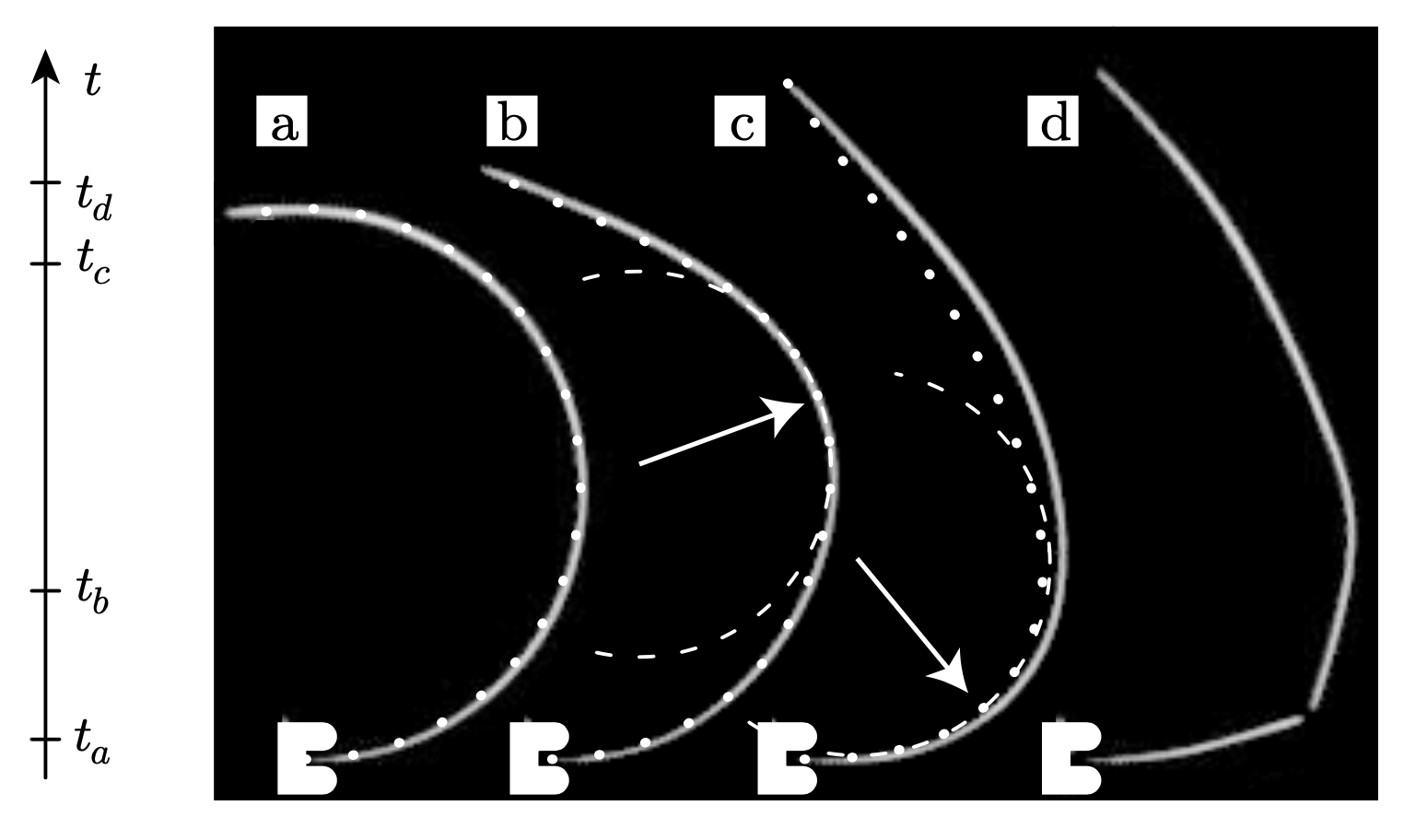
实验中采用的是Barilla 1号意面，长度为24.1厘米。意面被弯折成 （图3a）。为了捕获意面的快速变化过程，用来拍照的相机帧幅率为每秒1000幅。一端释放以后的中间态（b,c）可以看出震动波的产生，表现为意面局域曲率的变化。图3中点划线代表的是数值模拟预测的意面形状，虚线代表的是最大曲率位置处的内切圆。很明显可以看出，b和c中中间态的最大曲率超过初始的曲率(对应的自然是曲率半径的减小)。c对应的是一端释放后第一个断裂将要发生的时刻。这时，自相似系数和最大曲率位置都跟上面的解析解预测的一致：最大曲率点在 处，对应的曲率半径为 。d时刻为紧随c以后的断裂发生的时刻。我们也可以清楚的看到，断裂以后新的意面自由端的曲率迅速变为零（平直的意面），而新的震动波又得以产生。

这样，这一段意面又一分为二了，加上初始断裂时的另一段我们已经至少有三段了。其实只要新的震动波的强度足够，还会有更多的断裂。

【本人刚刚在厨房试了下，屡试不爽，总是很轻松的把意面掰的稀碎。】

文章最后一部分我就一笔带过了（否则看的人就越来越少了吧？）

最后改变不同型号（不同材质和半径）的意面，以及改变初始的曲率来重复图3的实验。结论是：断裂的发生对初始曲率非常敏感；在空间-时间相图( )上所有的断裂都集中在某些特定的区域（这是自相似性的体现）。

以上大概就是为啥意面总是断成多于两段的理论解释了。 理论好像总是有点枯燥。

不过MIT的PNAS工作^{[2]就有意思的多了。折成仅两段的方法评论区的部分朋友已经猜出来一半了，(有的人就是很聪明!)}

至于到底是什么方法？又是为什么？

您要是还有兴趣，请移步这里：

[走之前别忘左下角 ]

参考

1. ^Why Spaghetti Does Not Break in Half. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.95.095505
2. ^Controlling fracture cascades through twisting and quenching. https://doi.org/10.1073/pnas.1802831115