【知识仓库】力

发布时间: 2021-05-18 14:55:24 来源: 励志妙语作者: 爱XR的麦子栏目: 经典文章点击: 96

要想使用牛顿定律，就需要计算合力。要想计算合力，就需要了解各种力，这里有一些例子。接触力(ContactForce)：当两个...

【知识仓库】力

要想使用牛顿定律，就需要计算合力。要想计算合力，就需要了解各种力，这里有一些例子。

接触力 (Contact Force)：当两个物体相互接触时，原子会通过一系列电磁和量子现象相互作用，而产生的力。宏观上，动力学里接触力是支持力 (Normal Reaction) 和摩擦力的和。

静摩擦力 (Static Friction)：当有外力作用在一个静止的物体上时，外力的反作用力即为静摩擦力。但是存在一个最大的静摩擦力。

F_s leq mu_s F_N ，

F_s -静摩擦力， mu_s -静摩擦系数， F_N -支持力。

动摩擦力 (Kinetic Friction)：当物体开始运动后，摩擦力依旧差不多与支持力乘正比，但是摩擦系数大小会变。

F_k = mu_k F_N

F_k -动摩擦力， mu_k -动摩擦系数。值得注意的是动摩擦力不与速度或速度的平方成正比，这只在干燥的表面成立。

一般情况下， mu_s > mu_k ，也是因此，一旦物体运动起来了，会保持运动。

摩擦力相关的物理法则总结在Amontons' laws of friction。

重力 (Gravitational Force)： $F_g = frac{Gm_1m_2}{r^2}$ ，重力常数 $G = 6.674 times 10^{-11} Nm^2{kg}^{-2}$ ，重力为吸引力，方向沿着 m_1 和 m_2 质心的连线。

向量表示就是 $vec F_{12} = - frac{Gm_1m_2}{r^2} hat{r}$ ，此为 m_1 作用在 m_2 上的力，单位向量 hat{r} 从 m_1 指向 m_2 ，负号代表吸引。

质量 (Mass)，在继续讨论重力之前，必须认清一个概念：质量是什么？ F = ma 里的质量与 $F_g = frac{Gm_1m_2}{r^2}$ 里的质量一样吗？

假设它们是不同的，一个是“惯性质量” (Inertial Mass)， m_i ，一个是“重力质量” (Gravitational Mass)， m_g 。

那么在讨论一个物体掉落地球的过程中， m_1 = M_E ， r = R_E ， m_2 = m_g ，就有了

$F = m_i a = frac{G M_E m_g}{{R_E}^2}$ ，

这样的话

$a = frac{G M_E}{{R_E}^2} frac{m_g}{m_i} = g$ ，

如果说，这两个质量不是同一个值，那么 $frac{m_g}{m_i}$ 这个比值应该对于不同物体会有不同的结果，于是重力加速度也应该对于不同物体不一样。

但是， 对于所有物体都是一样的。目前的实验表明， $frac{m_g}{m_i} = 1$ 的精度可以到小数点后13位。因此，我们可以认为这两个质量代表相同的东西，即便从概念上它们完全可以是不一样的东西。这在牛顿力学中是个美妙的巧合，但是却是后来广义相对论的理论基础。

而 $g = frac{G M_E}{{R_E}^2} = 9.81 m s^{-2}$

质心

当一个系统中不止两个粒子时，对于每个粒子，作用在它上面的力可以用

$vec F_i + sum_{j ne i}{vec F_{ji}} = m_i vec a_i$ ，

其中 vec F_i 为施加在这个粒子上的外力，而 $vec F_{ji}$ 为这个系统中其它粒子作用在这个粒子上的内力。

于是，作用在这整个系统上的力可以表示为

$sum_{i}vec F_i + sum_{i}sum_{j ne i}{vec F_{ji}} = sum_{i}m_i vec a_i$ ，

由于牛顿第三定律， $sum_{i}sum_{j ne i}{vec F_{ji}} = vec 0$ 。因此所谓的“合力”，为作用在这个系统上的所有外力的和， $vec F =sum_{i}vec F_i$ ，就有了

$vec F = sum_{i}m_i vec a_i$ ，

当我们想把这个系统考虑成一个整体，用 vec F = m vec a 来表示时，

$m = sum_{i}{m_i}$

$vec a = vec a_{CoM} = frac{sum_{i}m_i vec a_i}{sum_{i}{m_i}}$ ，

又因为 $vec a_i = frac{d^2 vec x_i}{dt^2}$ ，就有了质心的位置向量

$vec x_{CoM} = frac{sum_{i}m_i vec x_i}{sum_{i}{m_i}}$ ，

牛顿第二定律可以自由的使用，只要用质心。

对于一个连续的物体，系统内的粒子数量 rightarrow infty ，单个粒子的质量 m_i rightarrow 0 ，上面的质心公式可以变成

$vec x_{CoM} = frac{int vec x dm}{int dm}$

重力完全一样的公式可以被用在两个均匀球体上，而依旧是它们质心的距离，力不变。而如果质量相同，一个均匀球体产生的重力场与一个粒子产生的重力场在外部看是一样的。

牛顿壳层定理 (Newton's Shell Theorem)：对于一个球形壳而言，总质量为，外部的重力场像是集中在球形壳的质心处，而内部的重力场在任何位置都为0

证明：

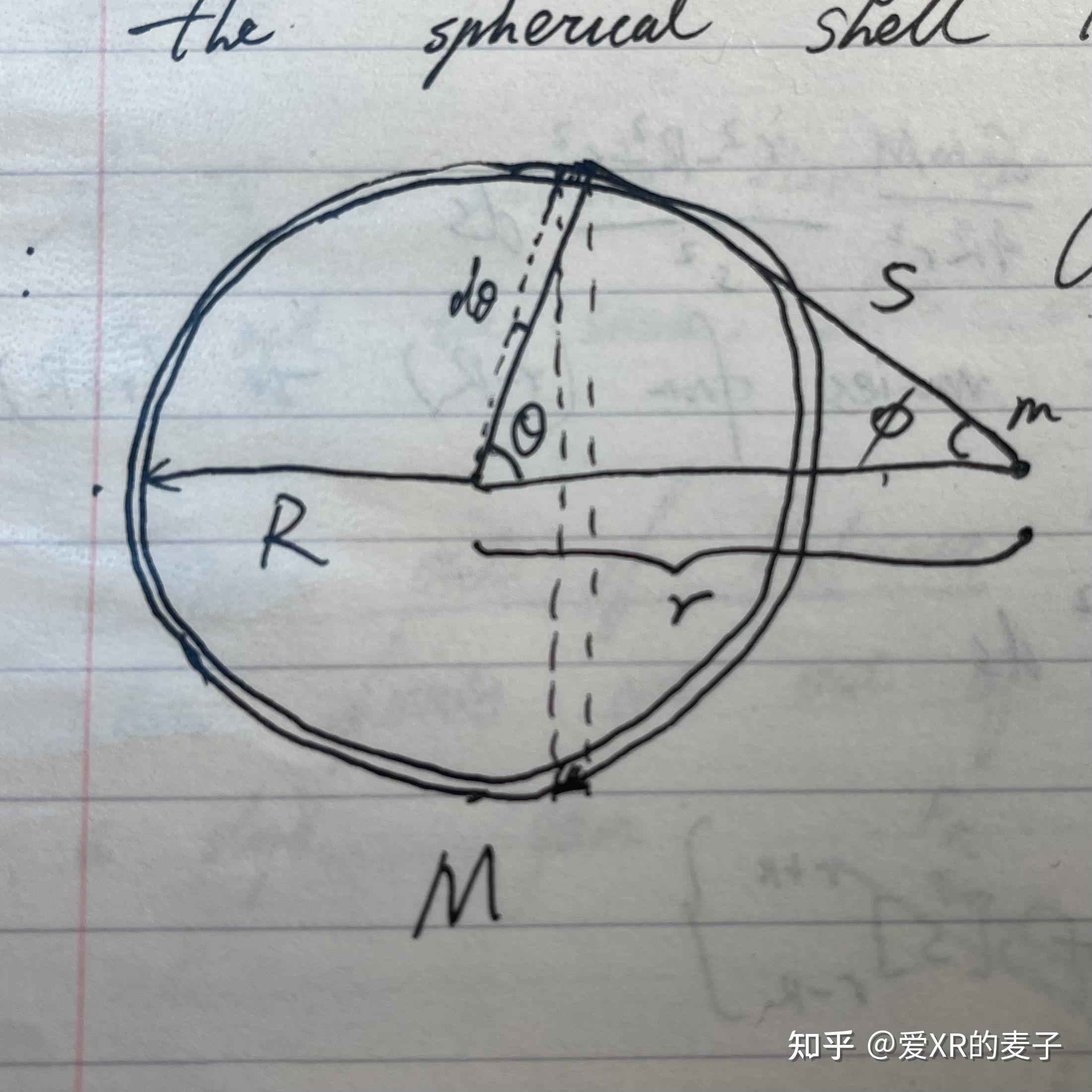
M为壳的总质量，R为壳的直径，r为空间内任意一点，m为测试质量点(test mass)，角度theta，phi如图所示，阴影为目标dM，注意图为截面，实际是球形壳

假设球形壳厚度忽略不计，质量分布均匀，定义一个表面密度， $sigma = frac{M}{4 pi R^2}$ ，图中阴影处的环的质量可以被表示为

$dM = sigma cdot 2pi R sin(theta) cdot R dtheta = frac{M sin(theta)}{2} dtheta$ ，

每个这样的环对测试质量点的力是对称的，那么在对称轴上由造成的力可以表示为

$dF = frac{G m dM}{s^2} cos(phi) =frac{G m M}{2s^2} cos(phi) sin(theta) dtheta$

通过cosine rule，

$cos(theta) = frac{r^2 + R^2 - s^2}{2rR} ; cos(phi) = frac{r^2 + s^2 - R^2}{2rs}$

这里面 theta, phi, s 都是变量，设为自变量，对 cos(theta) 进行求导，

$sin(theta) dtheta = frac{s}{rR} ds$

$Rightarrow dF =frac{G m M}{2s^2} cos(phi) sin(theta) dtheta = frac{G m M}{2s^2} frac{r^2 + s^2 - R^2}{2rs} frac{s}{rR} ds = frac{G m M}{4r^2R} frac{r^2 + s^2 - R^2}{s^2} ds$ ，

接下来为了得到整个力，对进行积分。

若测试质量点在壳外边， s in [r-R, r+R]

$F = frac{G m M}{4r^2R} int_{r-R}^{r+R} frac{r^2 + s^2 - R^2}{s^2} ds = frac{G m M}{4r^2R} (int_{r-R}^{r+R} frac{r^2 - R^2}{s^2} ds + int_{r-R}^{r+R} ds )$

$Rightarrow F = frac{G m M}{4r^2R} (left[ frac{-(r^2 - R^2)}{s} right]_{r-R}^{r+R}+ left[ s right]_{r-R}^{r+R})$

$Rightarrow F = frac{G m M}{4r^2R} ( -(r-R) + (r+R) + (r+R) - (r -R))$

于是最后得到了

$Rightarrow F = frac{G m M}{r^2}$

而如果测试质量点在壳里头， s in [R-r, R+r]

$Rightarrow F = frac{G m M}{4r^2R} (left[ frac{(R^2 - r^2)}{s} right]_{R-r}^{R+r}+ left[ s right]_{R-r}^{R+r}) = frac{G m M}{4r^2R} ( (R-r) - (R+r) + (R+r) - (R-r))$

因此

Rightarrow F = 0

壳外公式不变，壳内不受力，便有了牛顿壳层定理。

本文标题: 【知识仓库】力

本文地址: http://www.lzmy123.com/jingdianwenzhang/141238.html