01

如何科学预测恋爱走向

爱情的本质是什么，人们尚无定论，但是并不妨碍我们建立合（li）理（pu）的模型来预测一段恋爱的走向。

为了定量的描述一对情侣之前的亲密程度，我们定义一个指标，叫做亲密值，亲密值的大小与该对情侣的亲密程度成正相关，亲密程度越大则亲密值越大，反之则越小。

这个值会随着两者接触时间的延长而不断变化，理论上这个值应当是随时间连续变化的，但为了方便处理，我们将它离散化，也就是说每隔一段固定的时间亲密值发生一次变化，我们可以将每一个时间点得到的亲密值排在一起，形成一个数列。

比如第一天的亲密值为1，第二天的亲密值为2，如果亲密值增加说明两者亲密关系增强，如果在第三天亲密值变成了0.5，说明亲密关系变弱，有可能出现情感危机。好了，接下来我们正式开始进行分析。

首先，我们先进行定性的分析。

在一对情侣刚开始接触的时候，一般来讲亲密程度呈递增的趋势，设第n个时间点的亲密值为,那么在第n+1个时间点亲密值会增加，我们认为 （其中a>1)。但我们很快发现这样的设定是有问题的，这样亲密值将会是一个不断增大的等比数列，那么就不会有情侣分手了。

事实上，我们忽略了一项重要的因子，当两者的亲密程度不断增强时，会有一个耗散力。产生这种耗散力的原因有多种，一方面可能过高的亲密值会产生腻烦感，另一方面亲密值较高时两者的缺点会表现的比较明显。在罗兰·米勒的《亲密关系》一书中提到，“因为浪漫激情的三个重要因素——幻想、新奇、唤醒——一般会随着岁月流逝而减弱，所以浪漫的爱情亦会日渐消退”，所以不管怎样，反正爱是会消失的，对不对？

（虽然但是，我的心一直是冰冰的！）

在自然界中也有类似的现象，例如分子间的作用力（如下图），当两者相距较远时呈现吸引力，而两者相距较近时，两者间的作用力就会变成排斥力。

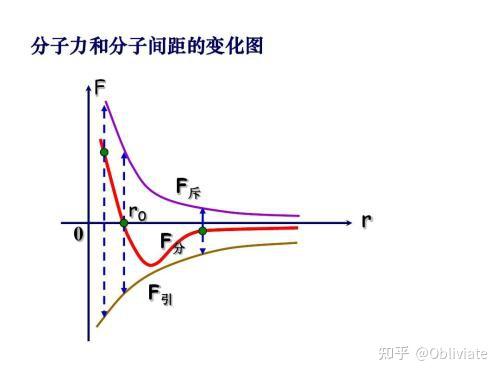
图丨分子间相互作用力

因此保持一定的距离是有必要的，否则会产生一定的排斥作用。

这一项排斥作用在亲密值较小时也较小，也就是当刚开始接触时两者之间的排斥较小，而随着亲密值增大这种排斥作用会不断增强，且增幅也变大。因此，我们可以认为这是一个二次函数，记为 。

总结一下，设第n个时间点的亲密值为 ,那么下一个时间点的亲密值为 ，其中第一项被称为驱动力，而后一项被称为耗散力。为了之后计算的方便，我们进行一次换元(令 )可以得到 。

到这里我们已经把最基础的模型建立完成了（但不得不说真的是非常粗糙），接下来要做的就是数值的分析了。

事实上，我们发现只要给定一个初始的亲密值，那么我们就可以不断的代入上面的那个等式当中，得出之后每一个时间点的亲密值了，也就预测这段恋爱的走向了。比如 但是这样的迭代并不直观，我们在这里引入一种较为直观的方法——“蛛网法”。

在这里我们首先画出二次函数 ，同时画出y=x。给定初始值 ，观察图中的A点，可以发现A的纵坐标正是 ，过A做x轴的平行线交y=x于B，B点的横坐标与纵坐标都是x1。再过B做x轴的垂线交二次函数于点C，其纵坐标为x2……经过反复这样的操作，过二次函数上的交点向x轴做垂线可以得到每一个时间点的亲密值，正如图中所得的 。通过这种方式我们就可以在图中直观的观察到亲密值的变化了。

接下来我们的问题就是亲密值的变化到底有什么规律。

我们可以看到亲密值的变化与这两个值有直接的关系——a和初始值。现在我们对这两个值进行分类讨论，可以得出有如下几种情况。

1.定常状态

第一种情况是在随着时间不断演化的过程中，亲密值最终会趋向于一个固定的值（在数学上我们把它称为不动点）。例如令 ，那么我们可以得到 将这些数据表现到图中，得到以下的图。

我们会发现最后亲密值会收敛到一个固定的值 。事实上为了得到这个值只需要令即可得到结果。（由极限的性质易得）对于一般的情况，可以得到 ，为了使定态值大于0，我们要保证a>1。

在这种情况下这段恋爱关系最终将会走向一个稳定的常态。

但是除了上一种的定态以外还有令一种。注意到是一个一元二次方程，还有一个解是0。这种情况下亲密值会随着时间不断的递减，最后会收敛于0（如下图所示）。

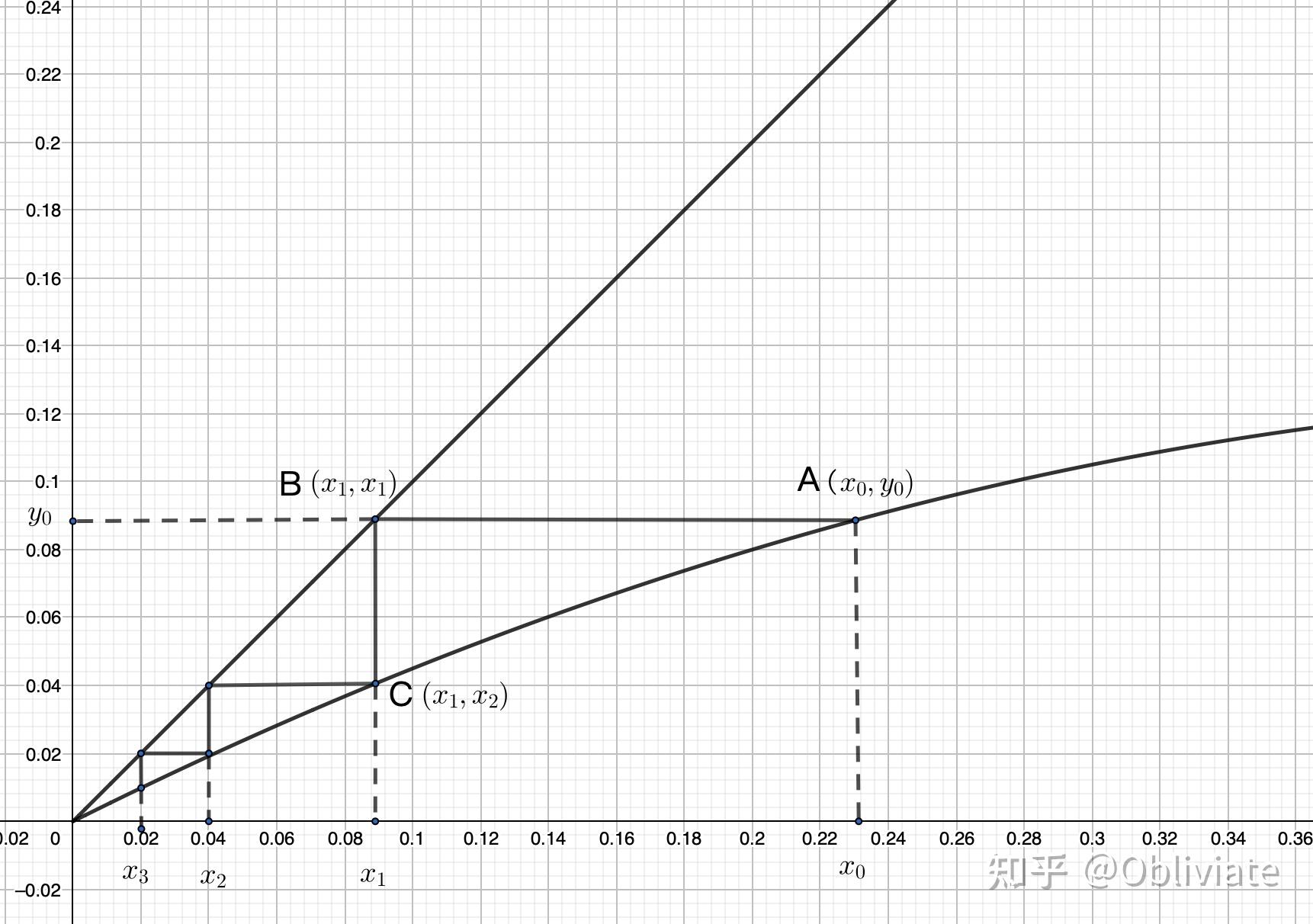
由此可以证明爱是会消失的。哦，当然也不一定是消失，可能只是发生了转移……

2.周期解

除了上面描述的最终收敛到一个定态以外，还有另外的可能，例如下图。

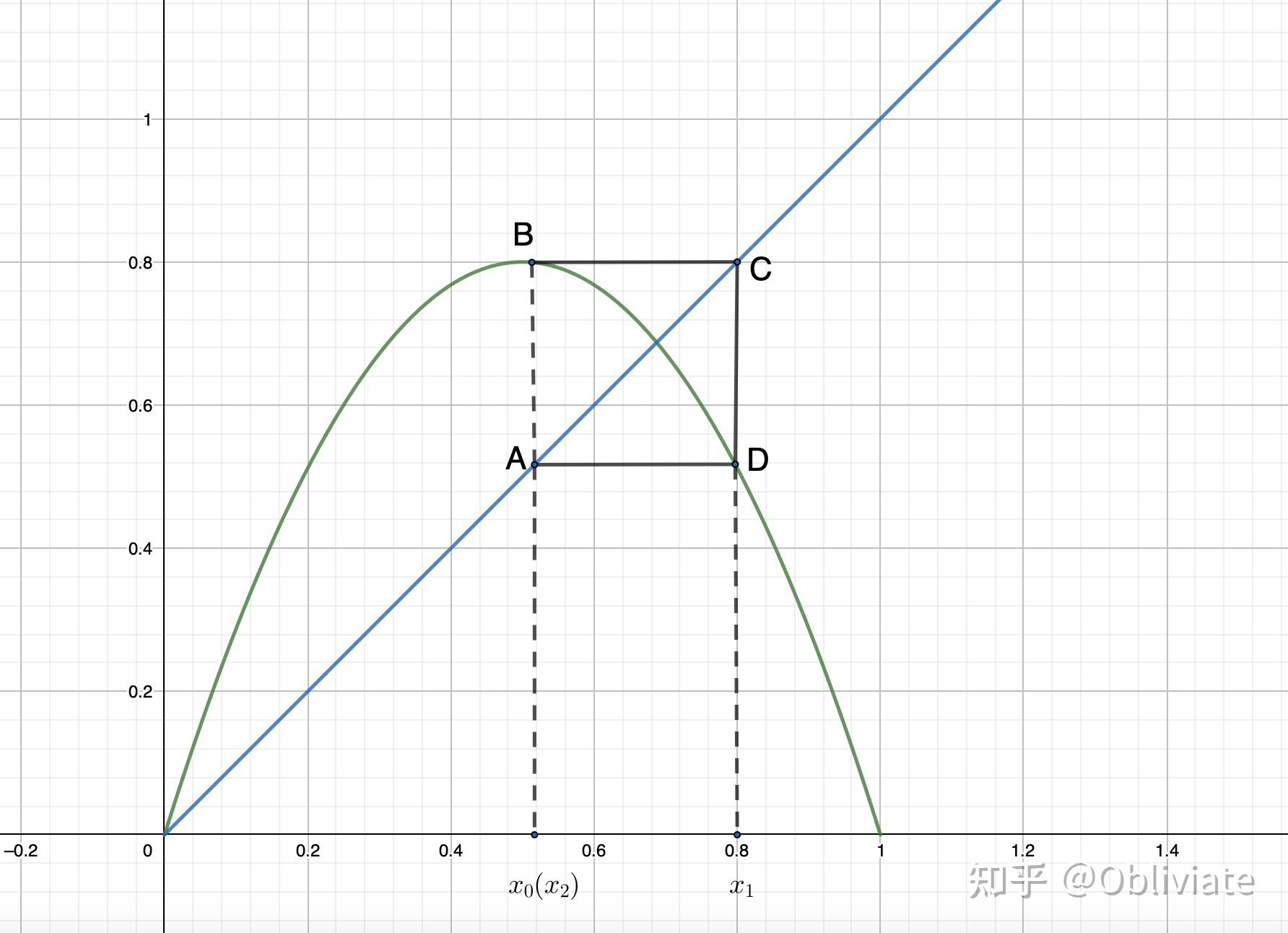
取 ，经过在图上进行迭代操作之后，发现两步之后回到了原始的位置。在这里出现了一个周期，也就是说，这对情侣的亲密程度将会呈现周期性变化。

要产生这种周期性的变化需要合适的a和 。接下来我们讨论固定a的情况下, 需要取成什么值。

在经过一次迭代之后x变成了，也就是，再经过一次迭代变成，要使其变回原来的位置，就要求满足。这是一个一元四次方程组，经过观察，我们发现是方程的解，也就是说0和 也是方程的解。一通计算猛如虎，我们可以得到如下方程， 。解为 。

上述经过两次迭代返回到原始值的情形我们称之为周期2，当然还可以有周期4，也就是迭代四次回到初始值，对应的方程为。除此之外还有8,16,32, 的周期,也存在像周期3、周期5这样的解。

3.混沌解

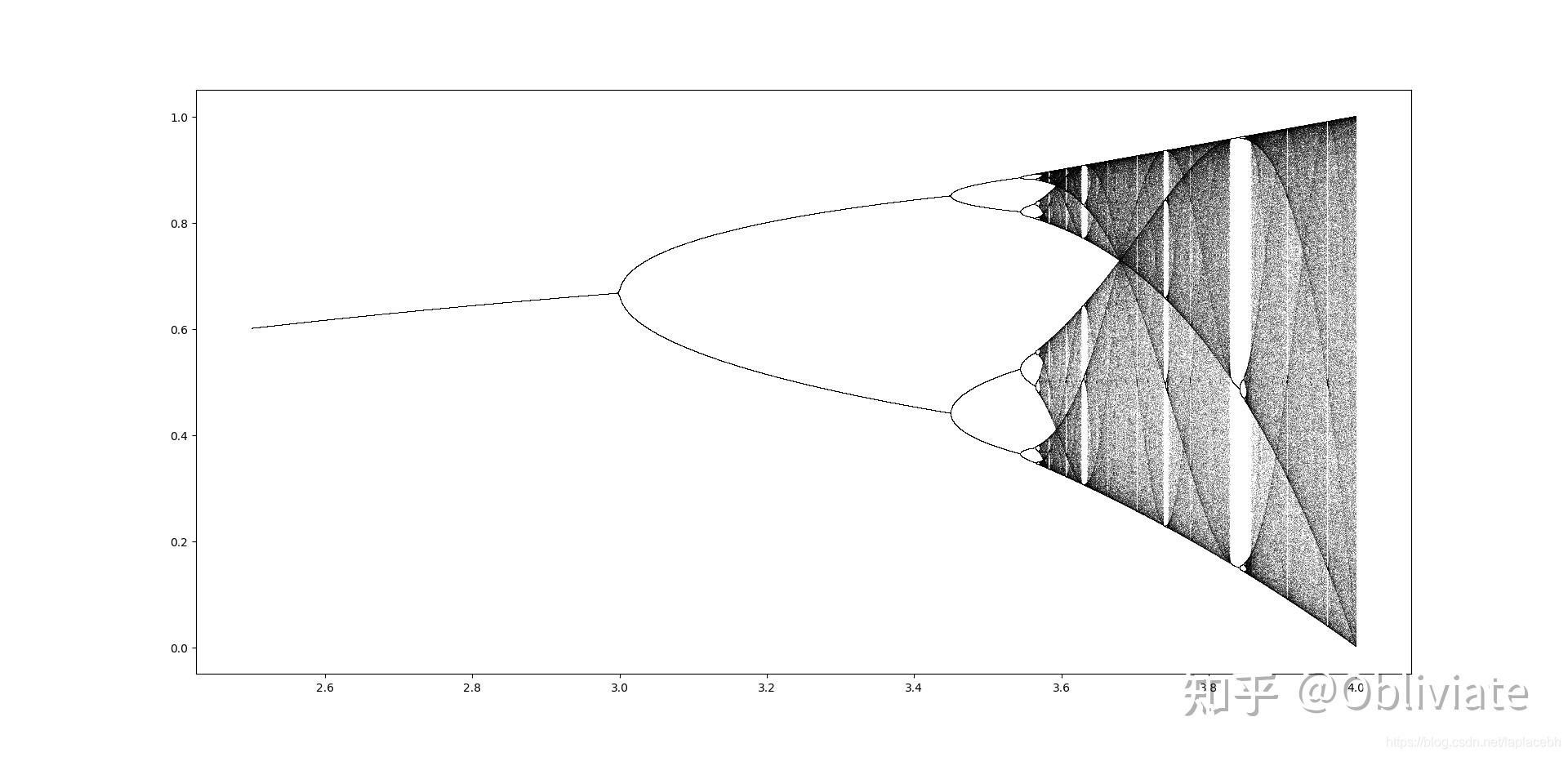
在上述讨论中我们可以看到，不同的a会产生不同的状态。要出现定常状态要求a满足0<a<3,出现周期2则要求a满足3<a<3.499,出现周期4时，要求a满足3.499<a<3.544,当a不断变化时，周期也在不断增加。经过计算表明，当a>3.56时，周期将趋于无穷大，也就是说没有一个固定的周期了，亲密值的变化变得没有规则，在这时候也就发生了所谓的“混沌现象”。如图，

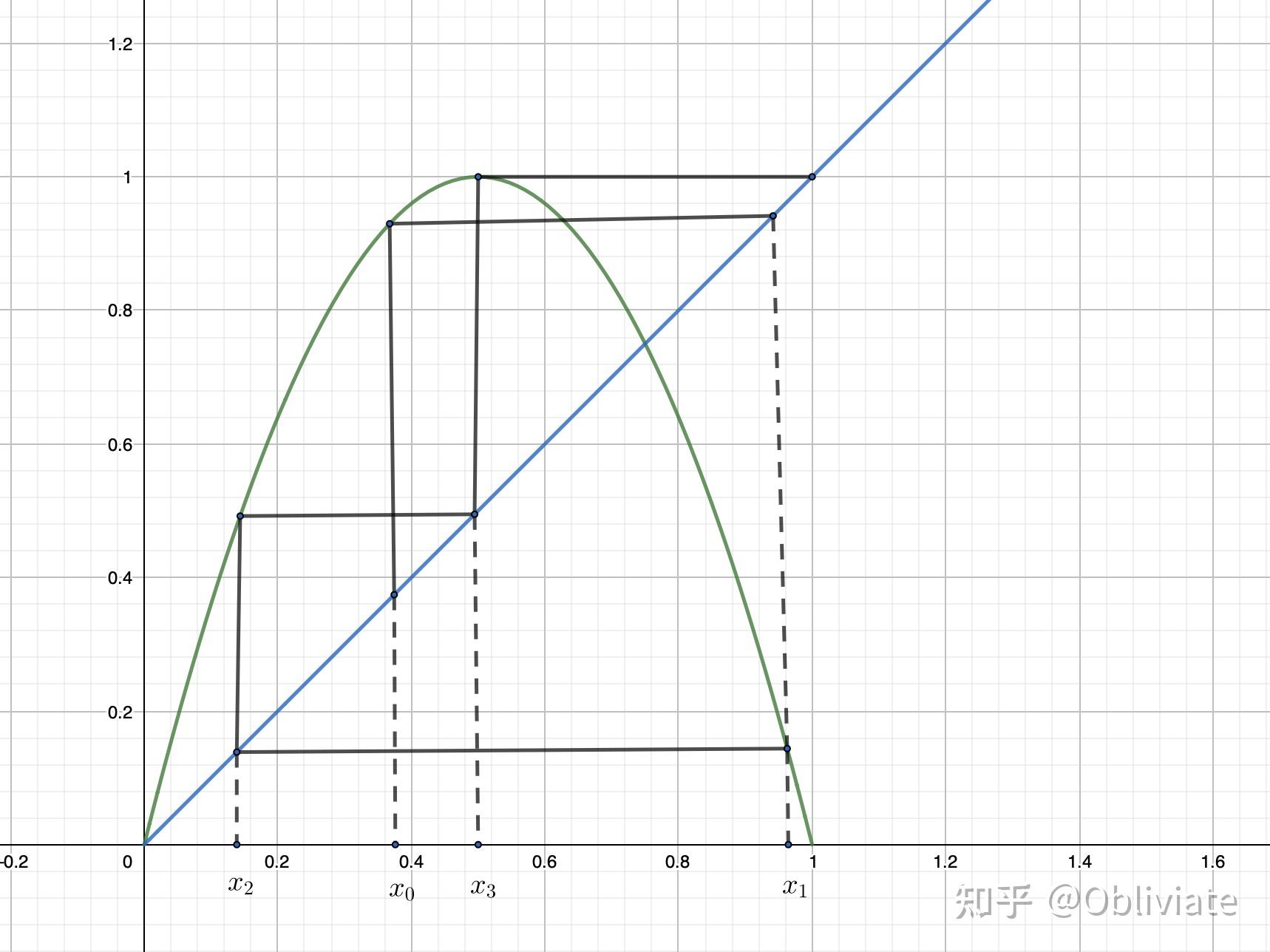
直观的来解释一下：与之前两种相对稳定的情况相比，这种类型的情侣的亲密程度是一个类似于随机的过程。一会儿闹着分手，一会儿甜的要死。与此同时，我们也要注意到在这种情况下，由于其不规则性，初始条件微小的偏差随着时间积累之后也会产生很大的不同。因此在这种状况下，他们的情感状态将是难以预测的。

所以，如果你的朋友中存在这种混沌状态的情侣，请务必小心，否则会发生以下现象。

而到最后你却会发现，他们分分合合玩得很开心，而小丑竟是你自己，毕竟很多人想失恋也没有目标……

到这里为止我们已经讨论完了所有可能的恋爱走向。

在上述讨论中，我们注意到其中系数a具有重要的意义，因为a决定了是可能哪一种情况的解。随着a的变化而导致解的不同的现象称之为分岔，将其直观的表现在图中，下图是分岔图。

02

什么是混沌？

在过去的物理学中，确定论占据着主要地位。所谓“确定论”，是指人们认为可以通过数理方程来对所有物体的行为进行预测，确定论的代表观点是法国科学家的名言：只要知道初条件就可以决定未来的一切。更为疯狂的是，其中法国数学家皮埃尔-西蒙-拉普拉斯提出一个假设，存在一种恶魔“拉普拉斯妖”，他知道宇宙中每个原子确切的位置和动量，能够用牛顿定律来展现世界的过去和未来。

图丨拉普拉斯妖

既然人体也是由各种原子构成的，在确定论的观点下，我们可以认为我们所有的行动都是由初始条件决定的，那么我们的人生走向也就完全被决定了，这让人不明觉厉。不过好在事实并非如此，这个世界比确定论要来的复杂得多。

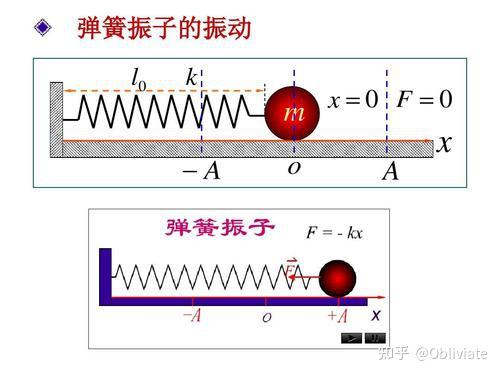
从现在的观点来看，确定论之所以可以统治物理学界这么久，主要原因在于过去研究的问题大多是简单的线性方程（指是状态量及各阶导数均为一次方的方程），研究的解也是单调的光滑的，一般只会出现简单的一些现象，例如最经典的简谐振动（如下图）。但事实上，我们现在遇到的更多的问题是更加复杂，其中伴随着复杂的混沌现象。

那么混沌现象为何会产生呢？

从之前我们对恋爱分析中可以看出，我们得到的递推函数是一条二次曲线，而不是一条简单的直线，这在数学中这被称为非线性的，而简单的直线则被称为线性的（这种说法并不是特别严谨，但是可以粗略的这么理解）。混沌现象产生的缘由就在于方程并非是线性的，在非线性的方程下，就可能会产生既不是定态，也非周期的混沌现象。

我们可以根据之前的分析总结出混沌现象有以下几个特点：

1.确定系统随时间演化出现不规则（类随机）现象。

2.该随机为系统固有属性，即内随机(intrinsic random)。

这也就是说这种类似的随机不是有外界的扰动导致的，而是由内在本身的结构决定的。

3.对初条件敏感。

初始条件小小的偏差，随着时间的变化则会产生巨大的不同。这其实是混沌现象中难以预测的主要原因。正是由于微小的偏差在最后会产生巨大的不同，再加上现实生活中我们又由于精度有限，难以准确获取这种微小的数据，最后导致预测严重偏离。

这种现象也被称为蝴蝶效应：“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国得克萨斯州的一场龙卷风。”

（之所以被称为蝴蝶效应其实是因为它的发现者洛伦兹所做的实验中的相图如上图所示，像一只蝴蝶。。。）

03

各种混沌现象

实际上，混沌现象在我们的生活中广泛存在。

例如在研究一个生态系统中种群的变化过程中，既有推动种群数量增长的驱动力，又有阻碍种群数量增大的耗散力（比如食物、竞争等）。假设第n年生态系统中某种群的数量为 ，那么下一年的种群数量为 。这个问题和上文中讨论的恋爱走向问题是完全类似的（这种问题在数学上抽象出来叫做逻辑斯蒂映射），在种群的变化中也同样存在定态解，周期解和混沌解。我们可以通过这种方式来合理的预测种群数量的变化。那么扩大到一个生态系统中，我们可以引入各种不同的种群，考虑它们之间的复杂的关系，进行合理的建模，从而预测这个生态系统的演化方向。

再比如天气预报问题。

大气状况是由确定的Navier-Stokes方程以及热力学方程所控制的，为了简化起见记为。该方程理论上只要给定初始条件，就可以预测接下来几天的天气状况。但是事实上由于混沌，能够较为准确的预报天气的日子只持续了五六天，之后就与预测的相差甚远了。（下图中两条曲线分别为预测的天气曲线与实际天气曲线）

另外，还有一个直观体现混沌的实验——小球反射。

如图是一个方形的球桌，小球碰到壁后反弹，我们描出小球的运动轨迹，标记为红色，之后再偏移一定的角度，再次描出小球的轨迹，发现两者仍然是相互接近的，也就是说对初始条件并不敏感，这是因为方形球桌是一个线性系统。

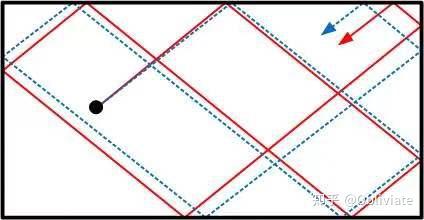
但是我们把方形球桌换成一个两面为弧形的球桌，仍然分两次射出小球，描出小球的运动轨迹。我们发现虽然初始状态只差了一点点，但是随着运动不断进行时，红色轨迹和蓝色轨迹分开的越来越多，这就是混沌现象。而产生这种现象的原因在于这是一个非线性系统。

（如上实验及图片参考知乎贾明子专栏中8、指数发散和蝴蝶效应，链接放在文末，感兴趣的同学可以去阅读）

除此之外，还有很多混沌现象。比如三体问题（指研究三个天体在相互作用下的复杂运动），地震预测（因此地震很难预测），还有股市（即便可以通过建模来分析，但由于混沌仍然难以准确预测股市走向）

图丨三体

04

结语

我们可以看到，相比于简单的线性系统，我们面对的是更加复杂的非线性的世界。而非线性理论也已是当今科学的前沿，因为人们不满足于线性条件的近似，试图用更加复杂的模型来研究解释这个世界。当然非线性的问题也更加的复杂，因为这些问题是没有解析解的，我们只能通过近似处理或者数据模拟才可以进行分析研究。

也许，人们对世界的认知永远是有局限的；也许，我们自以为建立的完美模型在上帝看来总是那么的简陋可笑。但是由于人类永远怀着对世界的好奇心，永远怀着不会终止的求知欲，我们从用宗教神话来解释我们所不能理解的事物开始，一路走来，到经典力学的建立完善，再到相对论、量子力学包括混沌理论的建立，越来越精确完善的理论正在不断提升我们对这个世界的解释力，同时我们也正在运用这些解释力来改变这个世界，甚至是创造世界，而这，也正是所有科研工作者所正在做和向往的事情。

从哲学的意义上来讲，我们永远不可能完全正确的认识这个世界，但即便如此，我们仍有理由相信，依靠人类的智慧和努力，理论的不断完善，我们将会越来越逼近这个世界的真相，越来越了解这个世界的本质所在。

感谢你能看这里，如果觉得这篇文章还不错的话，点一个赞吧！同时欢迎大家关注我的公众号，会有不定期的整活和科普哦

http://weixin.qq.com/r/HxNocIXEtdjKrcET90YN (二维码自动识别)

全文部分素材来源于网络，如有侵权请联系我删除。

本文参考：

《自然科学中的混沌和分形》，刘世达等，北京大学出版社，第二章第一节非线性系统的多样性，第二节驱动力和耗散力的竞争

《非线性物理概论》，陆同兴等，中国科学技术大学出版社，第二章离散系统动力学

《非线性动力学与混沌基础》，刘秉正，东北师范大学出版社，第二章离散映像

《亲密关系》，罗兰·米勒等，第八章爱情，浪漫爱情难以持久的原因

拉普拉斯妖，百度百科词条

贾明子：专栏8.指数发散与蝴蝶效应链接 贾明子：8、指数发散和蝴蝶效应