今天我们将手撕最速降线问题，即不用欧拉方程、不用变分硬解这个问题，当然，至少极限得学过，即本文适合学过极限的同学阅读。

最速降线问题即：

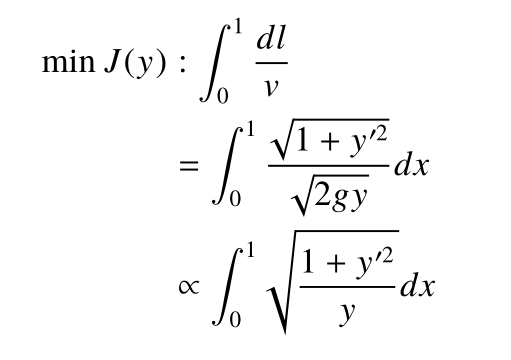
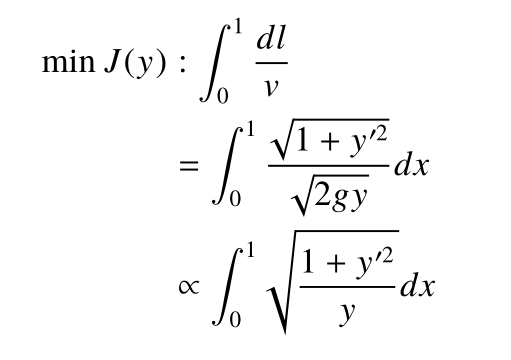
这里我们用J(y)表示由曲线y确定的时间，y是x的函数，J是y的函数，即泛函，最速降线目标即选择合适的y最小化泛函J。

当然y满足一些条件，比如两端固定，还有一定的光滑性。

求解的思想如下：

考虑某一固定的曲线y0，对于y0“附近”的其他曲线y=y0+th,（这里h表示任一段两端固定且光滑的曲线，t是一个小实数），J(y)-J(y0)会随着t的减小趋于某个数。而如果这个y0就是最速降线，J(y)-J(y0)会随着t的减小趋于0！这个极限其实也可以叫做导数，只不过是泛函对它的自变量——函数的导数。

具体计算比较繁杂，为了给大家展示思想，先来个简单的例子：

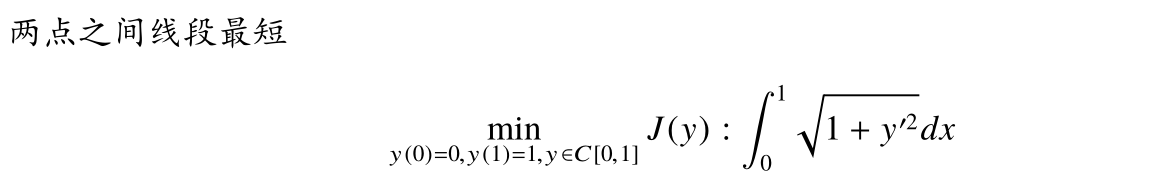
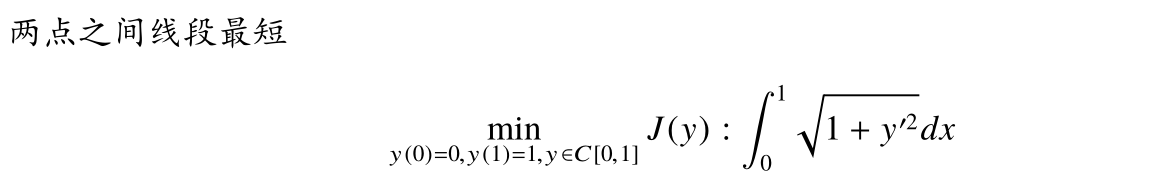
直接计算导数：

然后令导数为0，而h是任意的，这就意味着内积的后一项为0：

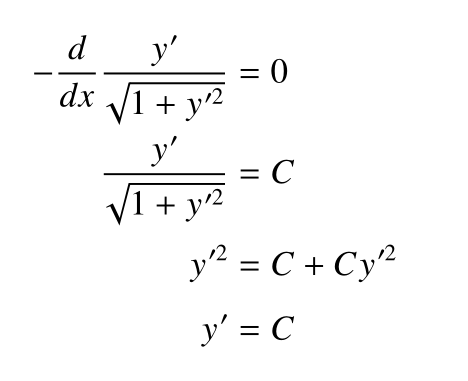
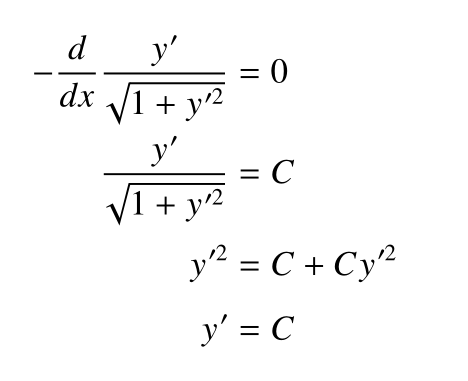
导数为常数正是直线的特征。

如此一来想毕大家已经熟悉这个过程了，

那么让我们开始手撕最速降线：

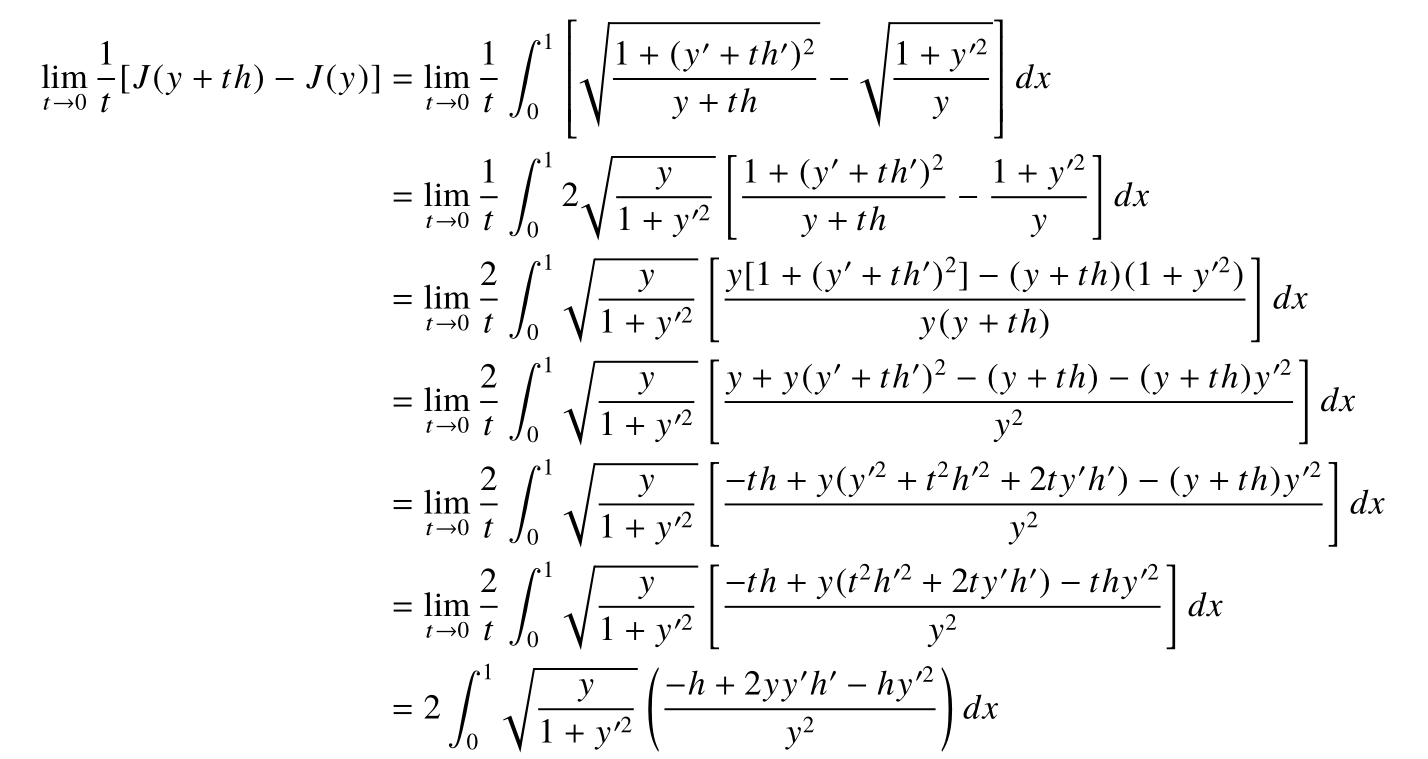
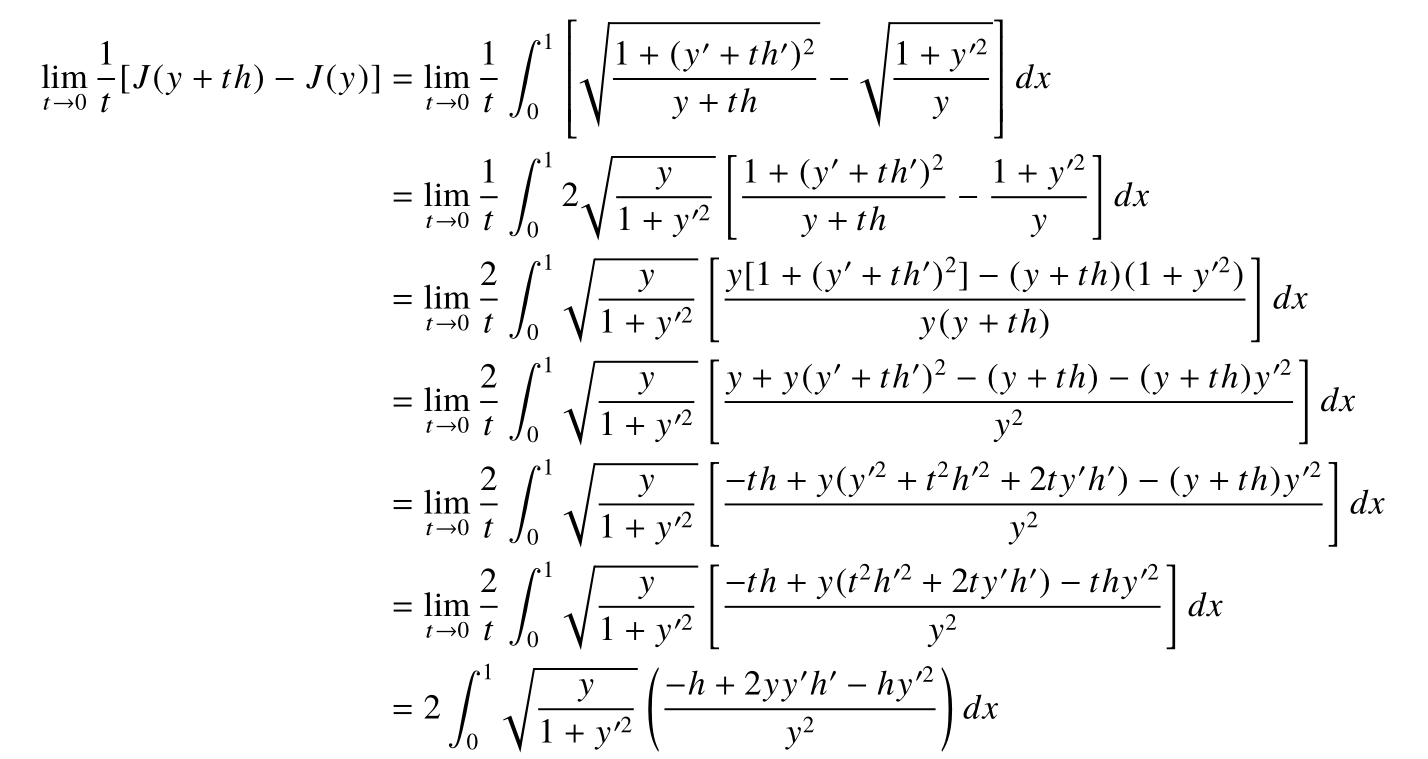
到这里是把t的极限算完了，为了把上式也写成h和另一项的内积，需要处理h'这一项，接下来的计算就是把含h'的项分部积分，h'就会变成h，边界项由于h也是两端固定的曲线本身就是0.

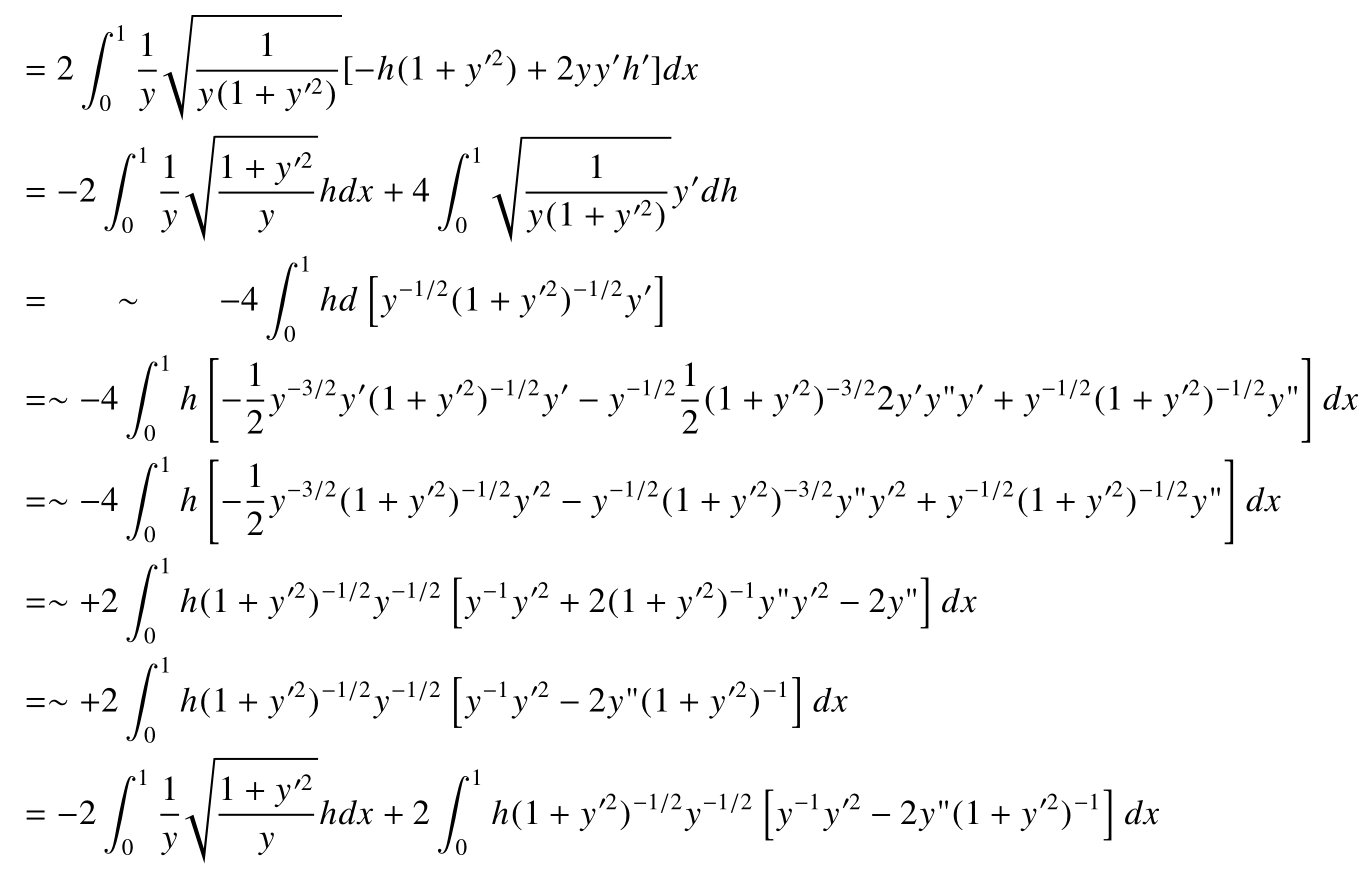
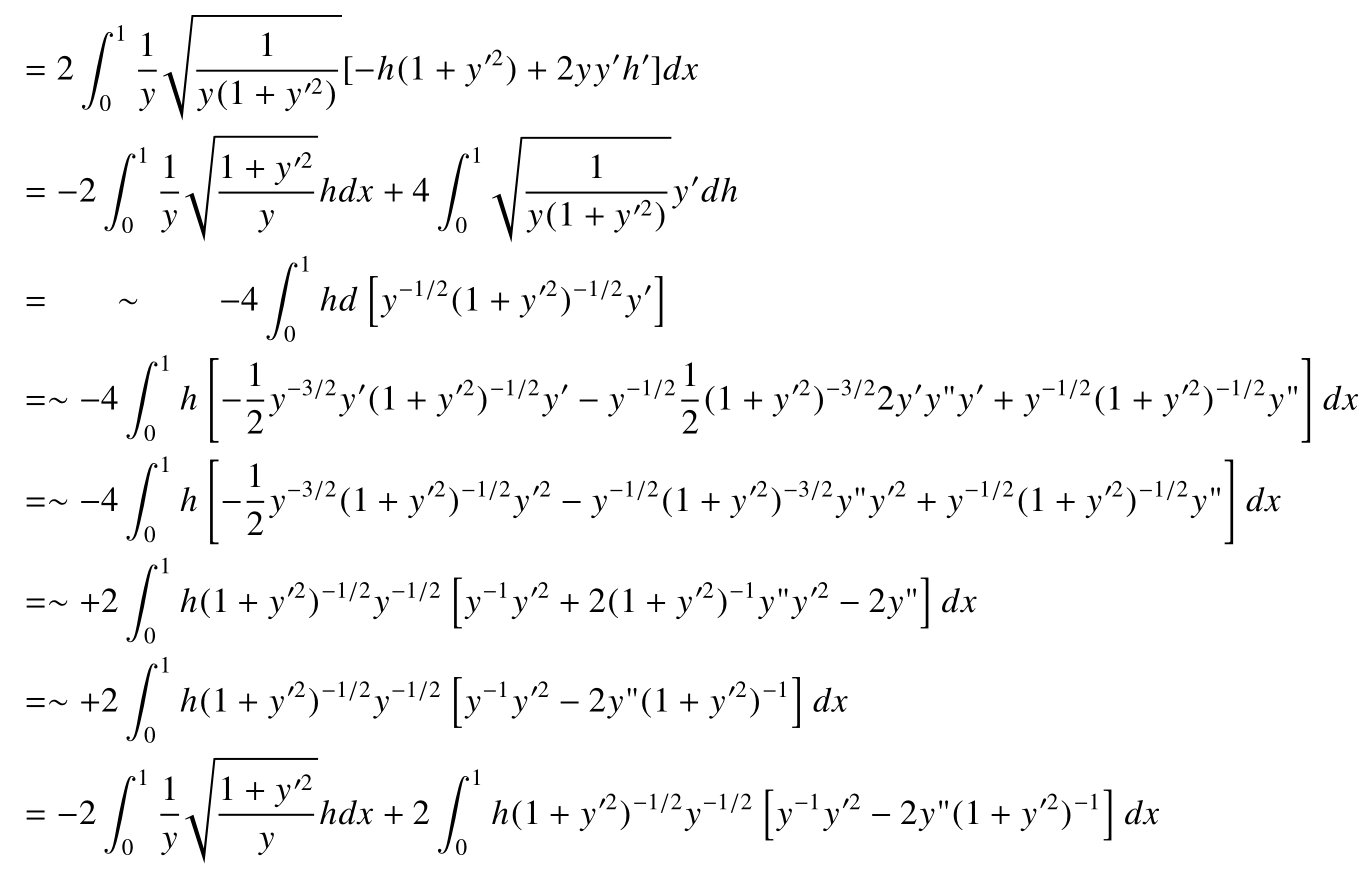
至此我们终于把积分里面的式子化成了h乘其他的形式，然后令导数为0：

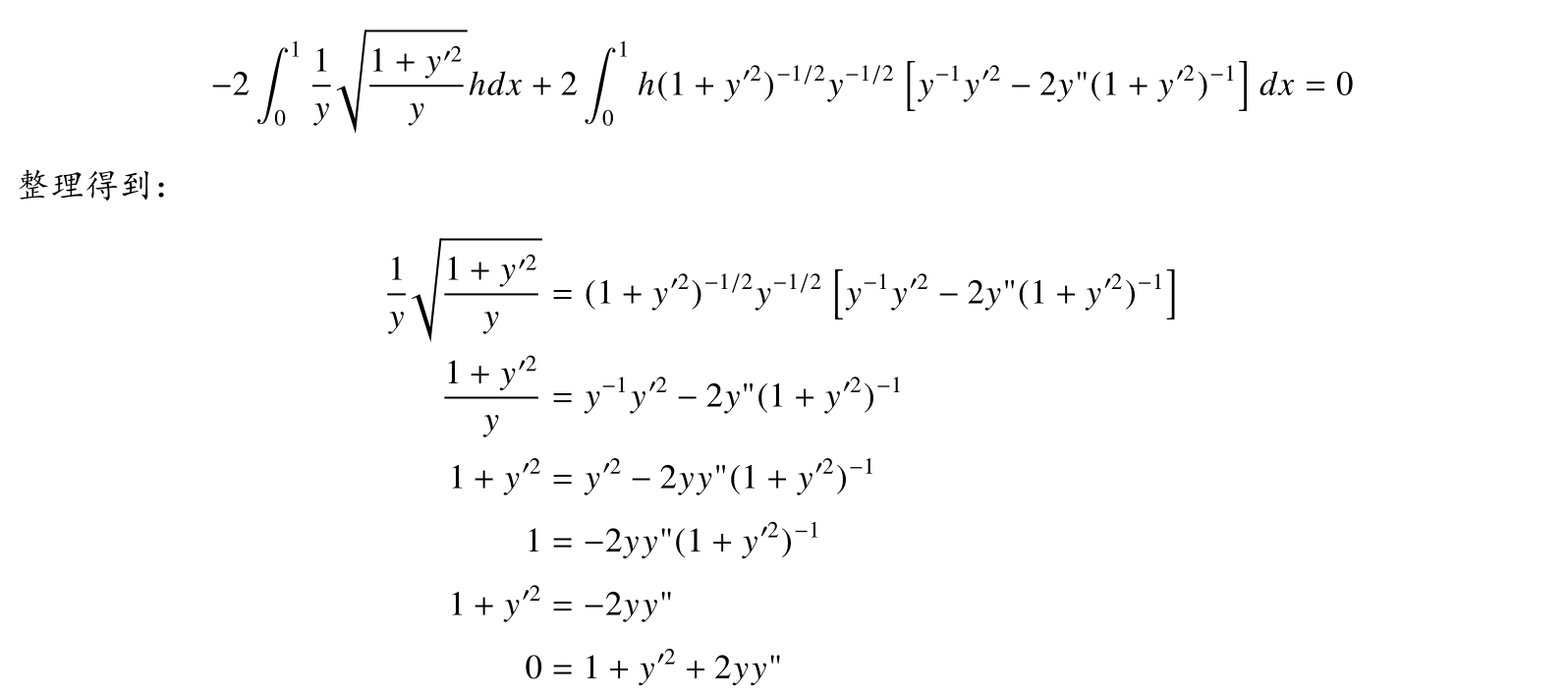
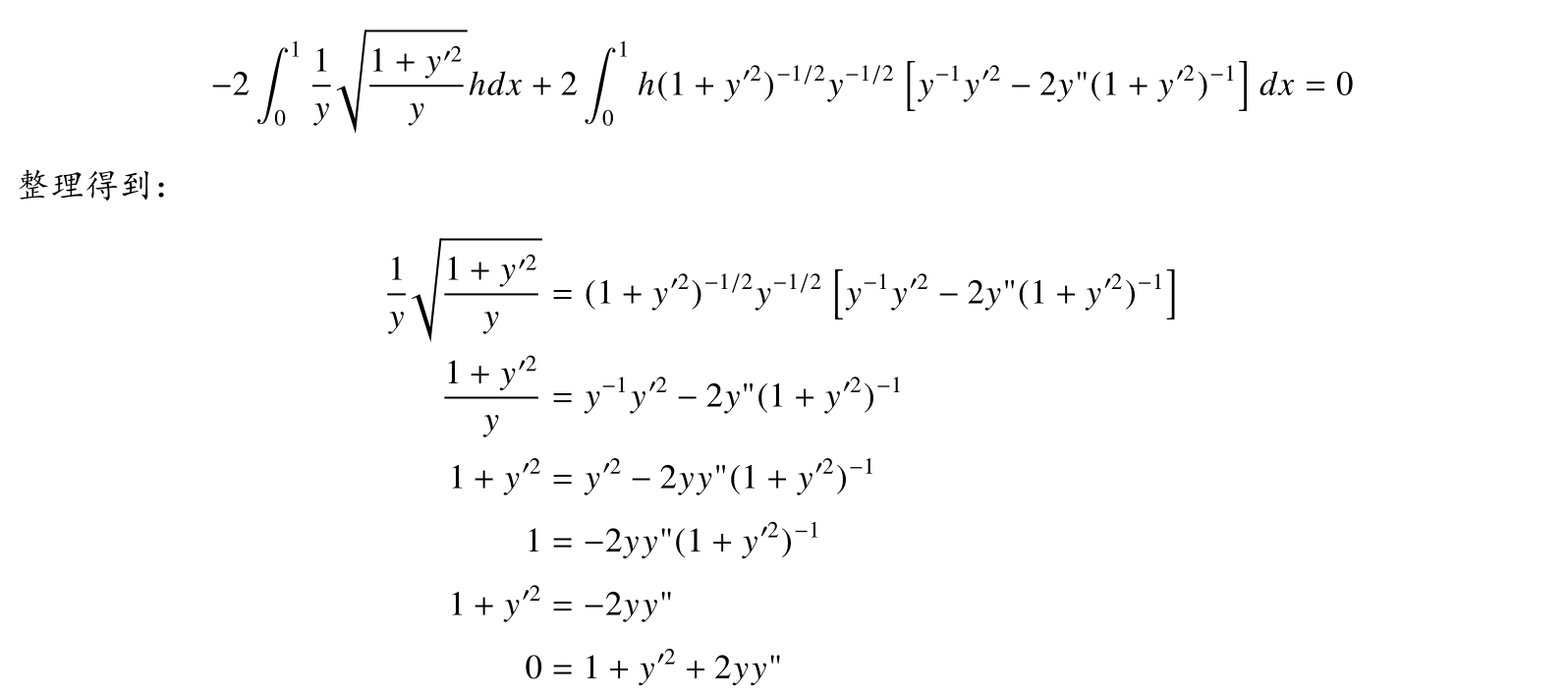
终于得到关于y的微分方程了，可是这个非齐次非线性的方程竟然一时间找不到解？

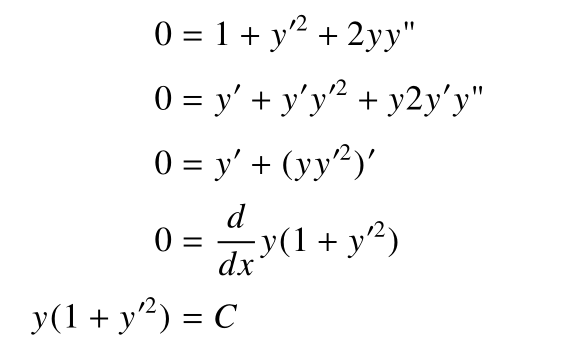
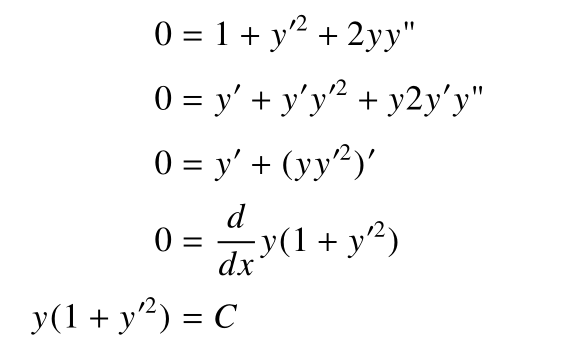
最后的微分方程了就是课本上大家熟知的形式了，继续解的过程就不赘述了。

正文到此结束！

那么写这么一篇文章的目的是什么呢？

其实本文带大家一起推了一遍欧拉方程，并算了个最速降线（我老早就想手撕这个了，但书上就告诉我要用欧拉方程、变分方法，让我很不爽）。学过泛函分析后，我总觉得已经可以干掉它了，今天也算完成了一个早有的小目标吧~

原文是用latex打的，不想在知乎里再输一遍，就直接截图了。

正文结束，如果对你有启发，欢迎点赞！

题后闲话：

什么叫手撕呢？我的观点是：用一些基本的定义解决问题就可以称为手撕了，比如有一些复杂极限用ε-δ语言直接证就是典型的例子。或者说不用现成的工具轮子自己推的做法就是手撕。这样好吗？就解决问题的效率而言确实不高，但就一个数学问题而言，我觉得是不错的学习方法。重剑无锋，大巧不工。不用什么定理解决问题靠的是扎实的基本功。以及， 这么做完总觉得挺爽的，有种心旷神怡的感觉。